PCMark04 как тест жёстких дисков. Первые впечатления.

Введение

Находясь в вечном поиске новых тестовых пакетов для исследования накопителей (о причинах - см. здесь) я не мог пройти мимо весьма интересного пакета PCMark04 от компании FutureMark, широко известной по серии тестов 3DMark. Тем более, что его уже успели "испробовать" некоторые мои коллеги...
Правда, некоторое время я скептически относился к самой идее тестов дисков в PCMark04, памятуя о крайне неудачной попытке использовать предыдущий пакет от FutureMark (тогда еще MadOnion) - PCMark2002. Но я по натуре - оптимист, да и один из стендов оказался свободен... В общем, я решил познакомиться с PCMark04 "поближе".

PCMark04

Из всего набора возможностей PCMark04 меня интересовали только тесты дисковой подсистемы. Согласно выложенному на сайте FutureMark pdf-файлу с описанием PCMark стало известно, что набор тестов дисковой подсистемы состоит из четырёх подтестов.
В отличие от PCMark2002, в новом пакете для тестов дисковой подсистемы применялись так называемые "трассы", то есть заранее записанные на некоем "референсном" компьютере треки дисковой активности. Для каждого подтеста был записана своя трасса, которую PCMark04 затем воспроизводит на винчестере испытуемого компьютера. Показателем быстродействия служит скорость обработки винчестером трассы, измеряемая в мегабайтах в секунду.
Для записи трасс была использована разработанная компанией Intel утилита RankDisk (вообще-то это делает программа WinTrace32, но в описании PCMark04 указана программа RankDisk...). Программа позволяет записать последовательность обращений к диску на низком уровне (т.е. на уровне драйвера контроллера) и, таким образом, при воспроизведении трассы мы получаем изолированную производительность жёсткого диска. Так, во всяком случае, полагают авторы PCMark04.

Программу RankDisk для "проигрывания" трасс обращений к диску давно используют самые авторитетные «тестеры» жёстких дисков – авторы сайта StorageReview, так что использование этой программы (или куска её кода) в PCMark04 можно только приветствовать.
Но авторы StorageReview воспроизводят записанные трассы на неотформатированном диске, что гарантирует абсолютно точную повторяемость «попадания» запросов к диску в ту область, в которую они были направлены при записи трассы. А создатели PCMark04, судя по тексту из pdf-файла, предлагают воспроизводить трассы на размеченном диске. При этом для тестов на нём создаётся так называемый «dummy»-файл, трасса пересчитывается для работы только внутри этого файла, и данным пользователя никакая опасность не угрожает. Но, увы, никто не может гарантировать, что временный файл будет расположен на диске в том же самом месте, в котором записывалась трасса. И еще более проблематичным будет добиться того, чтобы этот файл создавался "в одном и том же месте" на дисках разного объёма.
К тому же трасса должна содержать не только запросы к диску программ, но и всю дисковую активность операционной системы (обращение в swap-файл, ведение журнала и т.п.). Так что к фразе «file is created in the same (or closest possible) physical location of the target hard disk» стоит отнестись с известной долей скептицизма.

Конечно, я понимаю желание авторов PCMark04 дать возможность тестировать диски не только «профессионалам», но и конечным пользователям, но при проведении тестов на винчестере с установленной операционной системой не обеспечивается важнейшее требование к тесту – повторяемость результатов, так как тестируемый диск не изолирован от влияния операционной системы.
К счастью для людей, которые занимаются тестами "профессионально", PCMark04 позволяет проводить тесты и на неразмеченном диске.


Человека неподготовленного этот скриншот мог бы и испугать. :)

Итак, PCMark04 воспроизводит следующие режимы нагрузки на диск:

Windows XP Startup – Эта трасса содержит последовательность обращений к диску во время старта операционной системы.

Application Loading – В этой трассе записана дисковая активность при последовательном открытии и закрытии следующих приложений:

Microsoft® Word
Adobe® Acrobat® Reader 5
Windows® Media Player
3DMark 2001SE
Leadtek® Winfast® DVD
Mozilla Internet Browser

File Copying – Эта трасса содержит лог обращений к диску при копировании примерно 400МБ файлов. Увы, никаких подробностей о среднем размере файлов или об их количестве в pdf-файле не содержится…

General Hard Disk Drive Usage – эта трасса содержит данные о дисковой активности при работе некоторого количества широко используемых приложений. При записи трассы производились следующие манипуляции:

Открывался документ Microsoft Word, производилась проверка грамматики, файл записывался и закрывался;
При помощи WinZip запаковывался и распаковывался некий файл;
Над файлом производились операции шифрования и дешифрования с помощью программы PowerCrypt;
Набор файлов проверялся антивирусом F-Secure Antivirus;
Программой WinAmp проигрывались MP3- и WAV-файлы;
При помощи Windows Media Player воспроизводилось DivX-видео;
Программой Windows Picture Viewer просматривались фотографии;
и т.д. и т.п.

Для уменьшения времени проигрывания трассы она была подвергнута «сжатию» - длинные паузы между запросами к диску были уменьшены до 50 миллисекунд. Такое время было найдено экспериментальным путём, как минимальное время паузы, не влияющее на результат теста.

После проведения всех тестов жёсткого диска PCMark04 выдаёт некое значение производительности диска, вычисляемое по формуле

HDD Score= (XP Startup Trace × 120) + (Application Load trace × 180) + (File
Copy Trace × 28) + (General Usage × 265)

Столь замысловатая формула вычисления рейтинга объясняется очень просто. В финальный результат подтесты входят с разным весом. Например, скорость загрузки Windows имеет вес 25 процентов, скорость загрузки приложений имеет чуть больший вес – 28 процентов. Скорость копирования, наоборот, имеет самый маленький вес – 12 процентов. И, наконец, максимальный вес (35 процентов) получила скорость работы диска в «обычном» режиме использования (General Hard Disk Drive Usage).

Тестовая система и методика тестирования

Системная плата – Albatron PX865PE Pro II;
Процессор – Intel Pentium 4 2.4 ГГц;
Системный диск – IBM DTLA-307015 15 Гб;
Графический адаптер – Radeon 7000 32 Мб;
ОЗУ – 256 Мб DDR SDRAM PC2700;
Контроллер – Promise Ultra133 TX2;
Операционная система – Microsoft Windows XP Pro SP1.

Главным отличием тестовой платформы, которую пришлось использовать для тестов PCMark04, от нашей стандартной является использование Windows XP. Увы, для того, чтобы использовать этот тест мне пришлось нарушить один принцип - не использовать на тестовых платформах операционные системы Windows до выхода SP2... Всё дело в том, что дисковые тесты PCMark04 работают только под Win XP (что вообще-то странно, ведь RankDisk прекрасно работает на любых NT-подобных ОС).

Для тестов были использованы четыре "самых крутых" жёстких диска с IDE-интерфейсом, так как именно на супердисках и нужно проверять качество тестовой программы. Потому я взял 250ГБ-диск Maxtor MaxLine II (7Y250P0), диск WD2500JB и два диска Hitachi - HDS722525VLAT80 и IC35L180AVV207-1. Как Вы можете заметить, последний диск отличается от прочих объёмом. Плюс к этому он принадлежит к предыдущему поколению дисков (60ГБ пластины). Но объём кэш-буфера у всех дисков одинаков - 8МБ, потому мы сможем, во-первых, сравнить три 250ГБ-диска разных производителей между собой и сопоставить результаты тестов в PCMark04 с ранее полученными и, во-вторых, сравнить между собой скорость дисков Hitachi двух последних поколений.

Для тестов на исследуемых винчестерах создавался 32ГБ раздел, который форматировался в NTFS и FAT32 (т.е. я решил пойти на поводу у авторов теста и проверить его работу на отформатированном диске). Полученные результаты показали, что тест индифферентен к типу файловой системы на тестируемом диске (чего и следовало ожидать, учитывая используемый способ тестирования), так что в обзоре приводятся только половина полученных цифр (только для NTFS).

Для исследования повторяемости результатов PCMark04 для каждого диска проводилась серия из десяти тестов. Между тестами тестируемый диск дефрагментировался, далее компьютер перезагружался, и, после окончания загрузки, перед запуском теста выдерживалась пятиминутная пауза. Все эти меры предпринимались для уменьшения влияния операционной системы на результат теста.

Результаты тестов

Пожалуй, впервые я привожу такие подробные результаты... Скоро Вы поймёте - зачем. :)


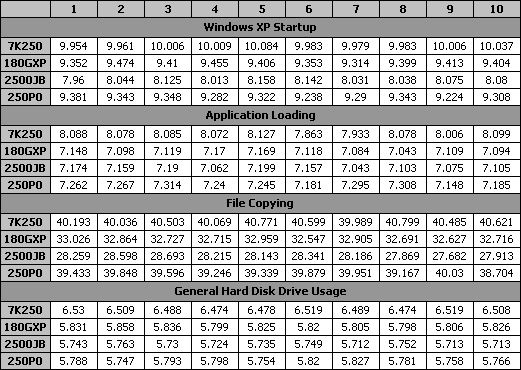
Итак, было проведено по 10 запусков каждого теста на каждом винчестере. После усреднения результатов отдельных попыток были построены диаграммы:


Трасса XP Startup была быстрее всего пройдена диском Hitachi 7K250 - может быть всё дело в его малом access time? Вот и результаты WD 2500JB это подтверждают. У WD 2500JB самый высокий access time среди всех участников этого тестирования, и он в этом тесте значительно отстал от всех...


С загрузкой приложений также быстрее всех справился Hitachi 7K250, а на последнем месте - Hitachi 180GXP - диск с наименьшей плотностью записи из числа участников.


При копировании файлов у нас образовались два явных лидера - диски Hitachi 7K250 и Maxtor 7Y250P0. Они заметно оторвались от Hitachi 180GXP и WD 2500JB. Что любопытно, это довольно хорошо согласуется с результатами наших тестов на скорость копирования. За исключением одной детали, но о ней - чуть позже.


При "генеральной" работе диска лидирует диск Hitachi 7K250. У него сегодня, похоже, бенефис...
Остальные диски выстроились лесенкой с очень маленькими ступеньками. Ну, очень маленькими...
Очевидно, что в некоторых тестах наши винчестеры показали довольно близкие результаты. Возникает вопрос - а достаточно ли повторяемы результаты дисков, чтобы таким образом судить о превосходстве в скорости одного диска перед другим. Другими словами, - а не проверить ли нам дисперсии...

Дисперсия, доверительные интервалы и все-все-все...

Для того, чтобы понять насколько "правильны" наши результаты, предлагаю немного погрузиться в мутные воды неглубокого озера моих познаний в матстатистике.

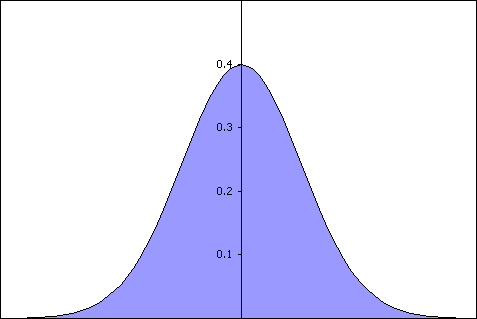
Как было совершенно справедливо отмечено в эпиграфе этого раздела, очень многие процессы случайного характера, в том числе и протекающие в природе, подчиняются нормальному закону случайного распределения Гаусса. Да и при тестировании жёстких дисков мы можем встретиться с проявлениями этого закона. Вот так, например, выглядит распределение случайного времени доступа (random access time) жёсткого диска.

Поэтому, сделаем допущение, что измеряемая нами Скорость диска = Истинная скорость + Ошибка, причём, Истинная скорость диска есть величина постоянная,а Ошибка, наоборот, носит случайный характер. Тогда, при заведомо большом числе измерений, распределение случайных значений Скорости диска будет нормальным.


Важнейшими параметрами распределения являются математическое ожидание M(x) и дисперсия D(x) случайной величины x. Обычно в задачах математической статистики параметры распределения случайной величины x неизвестны. В распоряжении исследователя имеется лишь выборка независимых экспериментов объёма n: [x1, x2,...xn]. В этом случае по выборке находят выборочные параметры, которые и служат приближением к теоретическим - генеральным параметрам. Приближение тем лучше, чем больше объём выборки n. В практических расчётах без большой погрешности можно принять, что уже при n>50 выборочные параметры совпадают с генеральными.

Рассмотрим более подробно эти параметры и их свойства.

Математическое ожидание непрерывной случайной величины задаётся интегралом:


Для дискретной конечнозначной случайной величины:

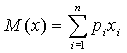
где x(i) и p(i) - отдельные значения и соответствующие им вероятности случайной величины, а n - число её возможных значений.

В частном случае равномерно распределённой конечнозначной случайной величины, имеющей n возможных значений

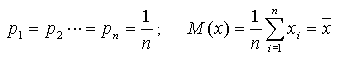
То есть математическое ожидание совпадает с понятием среднего арифметического. В общем же случае, когда вероятности каждого события не равны


математическое ожидание равно так называемому средневзвешенному значению дискретной случайной величины, в котором, при усреднении учтена разновероятность отдельных значений.

Говоря же простым языком, математическое ожидание - число, вокруг которого сосредоточены значения случайной величины.

Дисперсией D(x) случайной величины называется математическое ожидание случайной величины - [x-M(x)]^2. Для непрерывной случайной величины x:


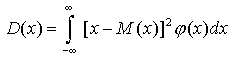
Для конечнозначной случайной величины, имеющей n значений


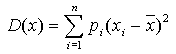
Дисперсию выборочной совокупности, состоящей из n значений случайной величины, вычисляют по формуле:

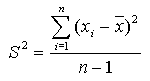
Эту величину принято называть выборочной дисперсией (S - от англ. слова Standart).

Дисперсия является удобной естественной мерой рассеяния случайной величины, поскольку в равной степени учитывает отклонения отдельных результатов от среднего, как в большую, так и в меньшую сторону и одновременно усредняет их по всем результатам.

Результаты многократного эксперимента и сопутствующие им случайные погрешности принято характеризовать с помощью двух статистических критериев:

ширины доверительного интервала [x1, x2], внутри которого могут лежать результаты отдельных экспериментов.
доверительной вероятности того, что они не выпадают из этого интервала.

В практике статистических исследований и при обработке результатов экспериментов распространённой является ситуация, когда случайная величина имеет заведомо нормальное или близкое к нормальному распределение (на всякий случай напоминаю, что мы это оговорили в начале раздела), но представляющая её выборочная совокупность имеет малый объём, т.е. не является достаточно представительной. Раздел математической статистики, посвящённый обработке малопредставительных выборок (2=<n<20), условно называют микростатистикой.
В основе микростатистических оценок нормально распределённых случайных величин лежит распределение Стьюдента, которое связывает между собой три основные характеристики выборочной совокупности - ширину доверительного интервала, соответствующую ему доверительную вероятность и объём выборки или число степеней свободы выборки f=n-1.
Вот так выглядит зависимость плотности вероятности от ширины доверительного интервала t в распределении Стьюдента при разном числе степеней свободы.


При f, равном бесконечности, наша кривая совпадает с кривой нормированного стандартного распределения. Но, чем меньше число степеней свободы, тем более пологий вид имеет график при больших значениях аргумента | t | (медленнее сближается с осью абсцисс). Отсюда следует, что при одинаковой ширине доверительного интервала доверительная вероятность, оцененная по Стьюденту, всегда меньше доверительной вероятности нормального распределения Гаусса-Лапласа. При этом, чем менее представительна выборка, тем больше разница в оценках двух типов.

Доверительная оценка среднего результата по Стьюденту имеет следующий вид:


где

- математическое ожидание среднего результата
- доверительная вероятность того, что случайная погрешность среднего результата из n независимых экспериментов не превышает .

Аналитический вид функции f(t) весьма сложен и громоздок, поэтому обычно пользуются таблицей заранее просчитанных коэффициентов Стьюдента. Для этого нужно знать только число степеней свободы f=n-1 и требуемую доверительную вероятность.

Ну а теперь, после крайне утомительного (не только для Вас, поверьте) экскурса в теорию, давайте вспомним, зачем мне понадобился аппарат матстатистики.

При сравнении средних значений скоростных характеристик винчестеров мне показалась подозрительной малая разница между ними. И сразу возник вопрос - а является ли эта разница статистически значимой? Так как редко какой тестер может позволить себе повторить тест винчестеров большое количество раз, то никто не может гарантировать, что на малой выборке (малом числе повторов эксперимента) значение среднего не сместится влево или вправо на некоторую величину... И тогда винчестеры с близкими значениями истинной скорости могут поменяться местами в рейтинге...

Итак, нам нужно получить некое значение ширины доверительного интервала, в который с доверительной вероятностью (возьмём, например, значение 0.95) попадёт среднее значение скорости диска, полученное по результатам 10-ти экспериментов. После получения ширины доверительного интервала мы посмотрим, а не пересекаются ли доверительные интервалы у различных винчестеров.

Для начала, посмотрим на зависимость S (среднее квадратическое отклонение, вычисляемое, как корень квадратный из дисперсии) от "типа теста"


Очевидно, что наибольший разброс результатов наблюдается при проигрывании трассы копирования. И, наоборот, самый маленький разброс получился у подтеста General Hard Disk Drive Usage. Интересно, связано ли это со временем проигрывания трассы? ;)

Для пущей научности, проверим, является ли различие дисперсий случайным или значимым. Критерий, который позволяет на заданном уровне значимости (1-0.95=0.05) определить, является ли различие двух дисперсий случайным или значимым, носит название F-критерия (критерий Фишера) и основан на распределении Фишера.
Рассчитанное значение F-функции для двух сравниваемых выборок находят, как частное S1/S2, причём в числителе должна находиться большая из двух сравниваемых дисперсий. Если рассчитанное значение F на заданном уровне значимости меньше значения Fкр, можно считать, что результаты экспериментов, представленные соответствующими выборками, равноточны.
Для того, чтобы упростить вычисления для каждого типа тестов мы возьмём выборки с максимальным и минимальным S, так как если эти результаты пройдут квалификацию по критерию Фишера, то и остальные выборки тоже будут квалифицированы.

Соответствующие расчёты показали, что наши результаты можно считать равноточными.

Ну а теперь нам осталось сделать только два шага...
Зная значения S, мы можем посчитать интересующий нас доверительный интервал. Проделав необходимые манипуляции, мы получили три значения скорости для каждого винчестера - среднее значение скорости по результатам экспериментов и минимальную и максимальную границу доверительного интервала.


Как оказалось, только в одном подтесте мы наблюдаем неопределённость.


Обратите внимание, что доверительные интервалы двух винчестеров "наложились". Точнее, доверительный интервал WD2500JB "включает" в себя доверительный интервал Hitachi 180GXP. Это означает, что несмотря на то, что усреднённое по результатам 10-ти экспериментов значение скорости WD2500JB выше, чем у Hitachi 180GXP, мы не можем утверждать (с вероятностью 0.95), что на другой выборке расстановка сил между винчестерами не изменится.

Воспользуемся t-критерием Стьюдента для проверки значимости различий средних значений результатов теста Application Loading дисков Hitachi 180GXP и WD 2500JB.
Согласно этому критерию, выборочные средние Xa и Xb значимо отличаются, если их разность превосходит своё стандартное отклонение более чем в раз, где - коэффициент Стьюдента для доверительной вероятности и числа степеней свободы объединённой выборки .
На практике обычно вычисляют значение отношения


где


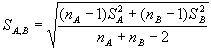
и сравнивают его с коэффициентом Стьюдента. Сделаем это и мы. :)

Полученное значение (0.530484) меньше, чем коэффициент Стьюдента (t=2.10), следовательно, средние результаты значимо не различимы.
Если же разница между этими винчестерами статистически неразличима, то может быть нам просто объявить их "равными по скорости" (в этом тесте) и перейти к выводам? :)

Вместо заключения

По результатам тестов дисков в PCmark04 мы можем выделить явного лидера - диск Hitachi 7K250. Остальные три диска показали примерно равные результаты. Впрочем, выделим высокую скорость диска Maxtor 7Y250P0 в "тесте копирования" и низкую скорость диска WD 2500JB в тестах XP Startup и "File Copying".

Теперь о применимости самого PCMark04 к тестированию диска.

Для начала проверим, соответствует ли этот тест требованиям, которые я сформулировал два года назад.

Тест должен иметь разумные размеры.
- Выполнено. По современным критериям 35МБ - не так уж и много (по сравнению с тем же 3DMark03).

Тест должен быть бесплатным для конечного пользователя.
- Не выполнено. Бесплатная версия теста даёт только суммарный индекс производительности, без подробных результатов по каждой подсистеме компьютера.

Тест должен работать под всеми распространёнными операционными системами.
- Не выполнено. Для того, чтобы полноценно протестировать компьютер, необходимо купить Windows XP. Особенно критично наличие WinXP для тестов жёсткого диска... ;)

Тест не должен иметь одностороннюю оптимизацию под продукты какой-либо одной фирмы.
- Пока у меня нет сведений о такого рода оптимизациях.

Тест должен выдавать "повторяемые" результаты.
- Что касается дисковой подсистемы, то тут вроде бы всё в порядке.

Тест и его результаты должны быть интуитивно понятны.
- Здесь я могу говорить только за себя. :) После прочтения pdf-файла и раздела FAQ на сайте FutureMark тест PCMark04 стал для меня интуитивно понятен.

Теперь стоит поговорить об адекватности результатов тестирования жёстких дисков. Полученные нами при помощи PCMark04 скоростные характеристики винчестеров, в целом, коррелируют с нашими представлениями о скорости современных винчестеров.
Однако результаты одного из тестов я хотел бы обсудить поподробнее. Согласно результатам PCMark два винчестера из четырёх при выполнении операции копирования показали скорость порядка 40МБ/сек. И это при том, что максимальная скорость чтения с этих дисков лишь немногим больше чем 60МБ/сек.

Насколько я понимаю процесс копирования, диск должен
1. Считать некое количество данных с пластины в буфер.
2. Передать их из своего буфера в память компьютера.
3. Передвинуть головки на тот трек, куда надо будет записать данные.
4. Поместить данные из памяти компьютера в свой буфер.
5. Выполнить запись блока данных.

Цикл 1-5 повторяется до тех пор, пока все данные не будут перенесены из точки A в точку B... Но, даже если предположить, что супер-умный и супер-быстрый винчестер не выполняет пункты 2 и 4 и мгновенно выполняет пункт 3, то скорость копирования не может быть больше половины от максимальной скорости чтения!
То есть для дисков со скоростью чтения 60МБ/сек. скорость копирования не может превышать 30МБ/сек. И это подтверждается результатами FC-test. Максимальная зафиксированная скорость копирования на текущий момент - 25МБ/сек.
А тут целых 40МБ/сек... Как говаривал г-н Станиславский: - "Не верю!" :)

Теперь о том, как всё таки проводить тесты дисков в PCMark04 (если проводить). Сравнивая результаты дисков, протестированных под NTFS, FAT32 и без разметки, должен сказать, что самые "чистые" результаты я получил на чистом диске (каламбур-ссс...). Чего, впрочем, и следовало ожидать.
Если сравнить абсолютные значения результатов дисков, протестированных в различных режимах, то необходимо отметить существенное снижение скоростей трёх из четырёх дисков (в режиме "без файловой системы") на тесте XP StartUp. Что это - влияние операционной системы или "особенности теста" - непонятно.

Итого:

C некоторыми оговорками тест PCMark04 можно использовать для тестов дисков.

Оговорки:

Диски лучше не размечать.
Тест копирования лучше не использовать.

Бонус

После столь неинтересной и, пожалуй, нудной статьи я предлагаю Вам немного расслабиться и оценить тонкий юмор известного американского статистика. Данная поэма лучше любого учебника познакомит Вас с основными понятиями математической статистики.

Отрывки из поэмы Кендалла М.Дж.
Перевод А.Дмоховского

Всюду славен Гайавата,
Он стрелок непревзойденный.
Легкий лук он поднимает -
Десять стрел взмывают к небу,
И последняя слетает
С тетивы тугой, звенящей
Прежде, чем вонзится в землю
Первая из десяти.
Все, кто видел Гайавату,
Говорили, что бесспорно
Совершенства он достиг

Но какой-то хитрый скептик
Тем не менее, заметил,
Что в стрельбе не только ловкость
Но и меткость ценят люди.
И добавил: было б лучше,
Если б славный Гайавата
В цель попал бы хоть однажды,
Пусть хоть выборка при этом
будет меньшего объема.
Гайавата рассердился
И сказал, что он в колледже
Посвятил себя науке,
Что статистикой зовется,
Он, себя считает в праве
Поучать своих собратьев,
Тут же лекцию прочел им.
Вспомнил он закон ошибок,
Усеченные кривые,
Информации потерю,
Заявил, что он добился
Не смещенных результатов,
И сказал, что после многих
Независимых попыток,
Даже если в их итоге
В цель ни разу не попал он, -
Все равно по средней точке
Отклонений от мишени
Можно сделать твердый вывод,
Что стрелял он безупречно
За возможным исключеньем
Пресловутой меры нуль.

Но упрямые индейцы
Возразили Гайавате,
Что они не понимают
Столь туманных рассуждений.
Им совсем не интересен
Результат его попыток.
И они предполагают,
Что охотник должен метко
В цель стрелять. А если будет
Он впустую тратить стрелы -
Должен сам за них платить.

Раздраженный Гайавата
Стал цитировать обильно
Р.А.Фишера и Итса,
Приводить работы Финни,
Книги Кемпторна Оскара,
Андерсена и Банкрофта.
Он взывал к авторитетам,
Убеждая несогласных,
Что в стрельбе всего важнее
Не прямое попаданье,
А научно безупречный
Статистический подход.

Кое-кто из возражавших
Согласился с Гайаватой,
Что в подобной точке зренья
Есть, возможно, доля смысла,
Но, пожалуй, все же лучше
Не пускаться в рассужденья,
А без промаха стрелять.

Наш герой в ответ на это
Предложил за луки взяться,
Чтоб строптивых оппонентов
В правоте своей уверить.
Он сказал: "Необходимо
Так построить состязанье,
Как советует учебник
Проводить эксперименты".
(Хоть научный этот способ
Применяется обычно
Для проверки качеств чая,
Но порою, как известно,
Приложим к другим вещам).
Гайавата разработал
Точный план соревнований,
Чтоб случайный их порядок
В соответствие пришелся
С тем характером, который
Носят множители в славной
Той теории, что ныне
Носит имя Галуа.

Те, кто выразил готовность
Состязаться с Гайаватой,
Были круглые невежды
В проведеньи испытаний,
И поэтому, наверно,
Все оставшееся время
Проводили в тренировках,
Соревнуясь меж собою
Или просто в цель стреляя.

И во время состязанья
Результаты всех стрелявших
Были просто превосходны,
Но, увы, за исключеньем
(Как не трудно мне признаться)
Результата Гайаваты.
Гайавата, как обычно,
Вверх свои направил стрелы,
Он так ловко это сделал,
Что остался не смещенным,
Но при этом, к сожаленью,
В цель ни разу не попал.

"Что ж, - сказали тут индейцы, -
Мы иного и не ждали".

Гайавата не смущаясь,
Попросил перо, бумагу,
Произвел расчет дисперсий
И в итоге вывел цифры,
Из которых стало ясно,
Что стрелки могли добиться
Лишь смещенных результатов,
А дисперсии при этом
Одинаковыми были
И совсем не отличались
От дисперсии, которой
Гайавата сам достиг.
(Правда, следует отметить,
Что последний этот вывод
Убедительнее был бы,
Если б в данных Гайаваты,
По которым вычислял он
Результат эксперимента,
Зафиксированы были
И прямые попаданья.

К сожаленью, оппоненты,
В вычислениях не смысля,
Не могли с героем спорить,
Что бывает очень часто
При анализе дисперсий).

Тем не менее, индейцы,
Не поверившие цифрам,
Отобрали у героя
Легкий лук его и стрелы
И сказали, что, возможно,
Гайавата в самом деле
Выдающийся статистик,
Но при этом совершенно
Бесполезен как стрелок.
Что ж касается дисперсий,
То какой-то грубый неуч
Произнес такое слово,
Что его сказать по чести
В статистическом изданье
Я не смею повторить.

И теперь в лесу дремучем
Бродит грустный Гайавата,
Непрестанно размышляя,
Вспоминает он нормальный
Тот закон распределенья
Отклонений и ошибок,
Что лишил его навеки
Славы лучшего стрелка.
И, порою, он приходит
К трезвой мысли, что наверно
Нужно целиться точнее,
Несмотря на риск смещенья,
Если все же в результате
Иногда ему удастся
Поражать стрелою цель.