Ваш город: Москва
DirectX9.0: Precomputed radiance transfer
Введение
В данной статье речь пойдёт о представленном в последней версии DirectX9.0 методе реалистичного динамического освещения сцены. Данный способ очень сильно отличается от известных ранее методов построения динамических теней на основе стенсил-буфера, который используется в известной не вышедшей игре Doom3, и метода проективного наложения текстур, который применяется для отображения теней от динамических моделей в современных играх. Плюсы и минусы вышеназванных современных технологий рассмотрены в соответствующем разделе данной статьи.
У нового метода есть две главные особенности: он позволяет строить в реальном времени приближённое к реалистичному освещение сцены с расчётом вторичного освещения, когда освещаемые объекты, подобно Луне, слегка отражают падающий свет. Позволяет рисовать блики, реалистичные размытые тени, учитывать распространение света в среде. Вторая особенность состоит в том, что, в отличие от современных методов, данный способ предполагает статичность сцены, но динамичность источников света. То есть, объекты сцены остаются неподвижными, в то время как источники света могут перемещаться. Правда, и тут есть ограничение, источники света могут быть только вне освещаемой сцены. Как движущееся по небу Солнце.
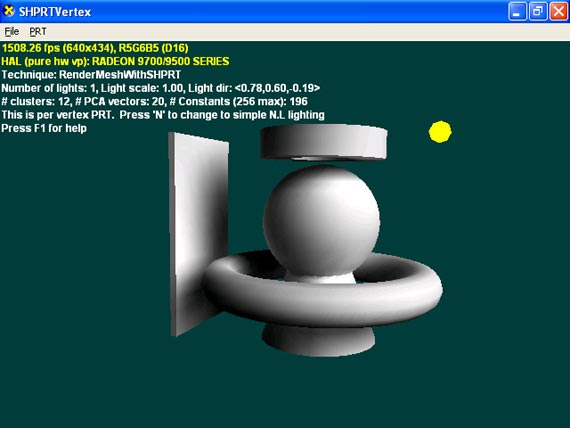
Сцена с движущимся источником света, освещение рассчитывается в реальном времени
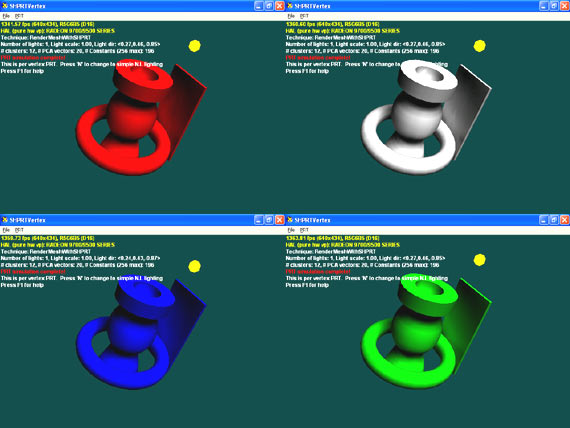
Вторичная освещённость. Объекты отбрасывают блики на тёмную поверхность. Всё это в динамике
Эти особенности обусловлены природой метода, базирующегося на предварительном расчёте распространения света внутри сцены. И уже с помощью найденных статических коэффициентов переноса излучения отображается динамическое освещение.
Описание
Итак, что же происходит? Пусть у нас есть статическая сцена, заключённая в воображаемую сферу. Представим весь приходящий свет как функцию на этой объемлющей (environment) сфере. Сфера представляет собой как бы совокупность всех возможных направлений, можно сказать, совокупность векторов единичной длины. И каждому направлению соответствует интенсивность излучения, приходящего по этому направлению. Там образом, можно задать входящее излучение. Для цветного излучения потребуются три компонента. Можно сказать, три сферы внешнего освещения.
Однако, эта функция освещения может быть достаточно сложной для нескольких источников света или при использовании объёмных не точечных источников света. С другой стороны, ни о каком расчёте распространения света по сложной сцене в реальном времени речи сейчас идти не может. Идея метода заключается в разложении меняющейся в реальном времени сложной сферической функции внешнего освещения по некоторому функциональному базису из заданных сферических функций, для которых заранее рассчитано освещение сцены.


Два графика сферических функций. Видно, что график закольцован
То есть, пусть у нас есть Lt(s) - определённая на сфере, то есть, на направлении, функция интенсивности внешнего излучения в момент времени t. Она, повторюсь, определяет интенсивность внешнего света, приходящего по направлению s в момент времени t. Зададим набор из N сферических функций, который будет базисом в пространстве сферических функций. Подобно как вектора e1=(1,0,0), e2=(0,1,0), e3=(0,0,1) являются базисом в пространстве трёхмерных векторов, и мы можем написать для произвольного вектора v разложение по этому базису v=v1*e1+v2*e2+v3*e3. Где v1, v2, v3 будут числами, а не векторами. В пространстве функций тоже часто можно ввести базис, и для некоторой числовой функции f(x) написать разложение по этому базису f(x)=f1*e1(x)+...+fn*en(x), где e1(x), ... , en(x) будут базисными функциями.
Мы написали разложение функции освещения в момент времени t в базисе постоянных сферических функций Y1, ... , Yn. Таким образом, в конкретный момент времени функция оказалась закодированной набором из N чисел.
Однако, пространство всех сферических функций бесконечно мерно, то есть, базис в таком пространстве состоит из бесконечно количества функций. Для точного представления некоторой функции потребуется бесконечная сумма вида
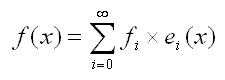
где fi - это бесконечная последовательность коэффициентов, а ei - это бесконечная последовательность базисных функций, i - индекс, который пробегает все натуральные числа. Поскольку функций существенно больше, чем натуральных чисел, выделение такого базиса имеет смысл. Так что, используя конечный базис из ограниченного количества элементов, мы сможем только приблизить исходную функцию. Таким образом, более правильно написать

Оставим за скобками вопрос о том, что, вообще говоря, не всякая сферическая функция может разлагаться в данном базисе. То есть, не всякую функцию можно достаточно точно приблизить линейной комбинацией элементов базиса. Но для непрерывных или кусочно-непрерывных функций, которые получаются при изображении реального освещения, можно подобрать конечный "базис", позволяющий качественно аппроксимировать исходную функцию. Естественно, чем больше функций в этом базисе, тем более качественное приближение можно получить.
Но для заданного внешнего притока света, соответствующего базисной сферической функции Yi, мы можем заранее в каждой точке сцены рассчитать освещение.
Интенсивность P освещения точки с координатами x есть функция F от координат точки x и внешнего освещения, заданного функцией Yi. Поскольку функцию освещения можно принять аддитивной и линейной, то есть, чтобы получить картину освещения от двух источников света можно отдельно вычислить во всех точках интенсивность освещения от каждого источника и сложить. И если интенсивность данного источника увеличилась, то пропорционально возрастёт освещённость всей сцены. Так могло бы и не быть при искусственных моделях освещения, когда, например, отражающая способность материала изменяется в зависимости от интенсивности падающего света. Но такие сложные модели ещё, конечно, рано рассматривать.
Мы можем написать интенсивность освещения в каждой точке в момент времени t.
Воспользуемся линейностью функции F. Эти функции Yi как бы соответствуют некоторым источникам света, на которые мы можем разложить сложное входящее освещение.
Напомню, что Li - это вещественные числа, коэффициенты разложения функции внешнего освещения L по базисным сферическим функциям Yi в момент времени t. Заметим, что F(x,Yi) не зависит от момента времени t и текущей функции освещения. Они зависят только от геометрии сцены и отражающих способностей элементов сцены. Эти числа называются коэффициентами переноса излучения (radiance transfer coefficient). Вот эти коэффициенты можно заранее вычислить для каждой точки поверхности элементов сцены. После этого в каждый момент времени остаётся только разложить текущую функцию внешнего освещения по базисным функциям Yi. Это не очень сложно и трудоёмко, если функций Yi не очень много. С другой стороны, их и не может быть много, так как тогда для каждой точки сцены придётся хранить слишком много информации, слишком большой массив коэффициентов. И набор этих функций Yi выбирается не произвольно, а наиболее оптимальным образом (чтобы было удобно по ним разлагать и т.п.). Эти функции Yi на самом деле берутся взаимно ортогональными, подобно базисным векторам e1, e1, e3 обычного трёхмерного пространства. Ортогональны они, естественно, в смысле скалярного произведения на множестве функций на сфере. Скалярное произведение двух функций в данном случае - это просто интеграл по сфере от поточечного произведения этих функций. Свойства данного скалярного произведения аналогичны обычному. Но это, собственно, имеет только косвенное отношение к рассматриваемой технологии.
DirectX 9.0
Рассмотрим теперь поддержку данного метода в новом DirectX. Ранее Direct3D была не более, чем интерфейсом между приложением, видеодрайвером и видеокартой, в ней содержались только сервисные функции преобразования данных и управления. Могли выполняться только простейшие расчёты по, например, нахождению нормалей к граням и т.п. В новой "ПрямойТрёхмерности" появился целый высокоуровневый engine для реализации данной технологии динамических теней. Программисту практически ничего не надо делать, кроме как вызывать соответствующие функции и задавать параметры.
Метод имеет две интерпретации - пиксельную и вертексную. В первом случае коэффициенты переноса излучения записываются в специальную текстуру, и на этапе рендеренга пиксельный шейдер считывает из текстуры коэффициенты F и вычисляет для каждого пикселя вышеприведённое значение Pt(x). Причём, числовые величины Li(t) постоянны для всех пикселей, поскольку зависят только от внешнего излучения в данный момент. Они передаются в шейдер просто как константы.
В случае вертексного освещения коэффициенты F(x) рассчитываются по вертексно. И вычисление выражения Pt(x) происходит в вертексном шейдере.
В состав DirectX SDK входит специальная программа для предварительно вычисления коэффициентов переноса излучения и записи их в файл для дальнейшего использования приложением. Рассмотрим параметры этой программы, она имеется в двух вариантах, рассчитанных для пиксельных и вертексных шейдеров.

Тут всё довольно просто. Первый параметр input mesh - это имя файла с анализируемой моделью. Order of spherical harmonic approximation - этот параметр отвечает за количество базисных сферических функций Yi. Для ускорения расчётов и достижения наилучшей аппроксимации из теоретически возможных, используются базисные функции специального вида, spherical harmonic. Их может быть только N2. Вот N и задаётся, в данном случае N=6, то есть, используется 36 базисных сферических функций.
Number of rays. Для нахождения интенсивности освещения данной точки сцены, в данном случае, некоторой вершины, используется модификация метода обратной трассировки лучей. Из точки в различных направлениях испускаются лучи, моделирующие распространение света. Они путешествуют по сцене, отражаются, преломляются и т.п., некоторые из них покидают сцену. Вот они моделируют в обратном направлении путь света от внешних источников света, аппроксимированных сферическими функциями, до данной точки сцены. Понятно, что чем больше лучей мы обсчитаем, тем с большей точностью найдём коэффициенты переноса излучения. Но большее количество лучей потребует и пропорционально большего времени на предварительный расчёт сцены. Однако, количество лучей никак не влияет на время работы непосредственно программы, и на объём хранимой информации.

Луч выходит из точки и путешествует по сцене, отражаясь от объектов, пока не вылетит наружу
Number of bounces. Этот параметр отвечает за максимальное количество отражений от поверхности одного луча. Это нужно для расчёта вторичной освещённости, когда свет отражается от объектов сцены и освещает места, в которые не может попасть прямо. Как в помещении, если солнце светит в окно, освещён не только прямоугольник на полу, но вся комната наполнена светом. В случае нулевого значения будут рассчитываться только тени от объектов. Понятно, что значение этого параметра тоже влияет только на время предварительного расчёта сцены. Так что есть соблазн выставлять его всегда по максимуму.
Light scale задаёт масштаб сцены, соответственно, интенсивность поглощения света внутри объектов. Чем меньше масштаб, тем больше предметы просвечиваются лучами.
Subsurface scattering. Флажок определяет, будет ли рассчитываться распространение света внутри объектов сцены. Можно же считать объекты сцены частично прозрачными, и моделировать прохождение света сквозь них. При этом учитывать поглощение света и рассеяние. Эти две физические величины задаются параметрами Absorption coefficient и Reduced scattering coefficient в панели Material settings - Свойства материала. В данном случае эти значения считаются постоянными для всей сцены, но, в принципе, их можно устанавливать отдельно для каждого объекта сцены. Опять можно с радостью отметить, что такие эффекты не влияют на время работы программы, а только увеличивают время предварительного анализа сцены.
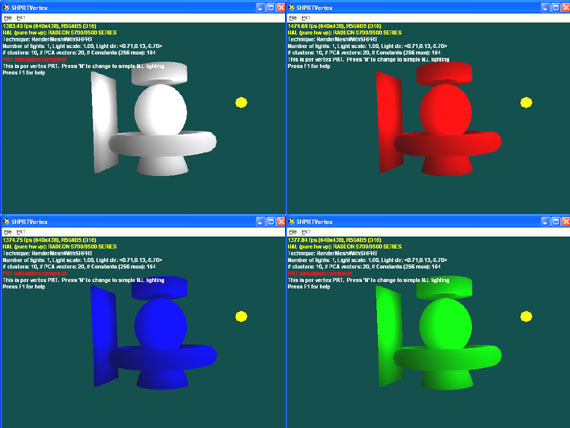
Объекты сцены полупрозрачны. Вместо отбрасывания тени сфера работает, как линза, фокусируя лучи
Данные параметры материала сцены, а так же Diffuse reflectance coefficient - коэффициент диффузного отражения - можно устанавливать отдельно для каждого цветового канала (флажок Spectral). Тогда появляется возможность сделать сцену прозрачной только в синем цвете, например. Или объекты сцены будут отбрасывать красноватые блики. Но эта возможность уже требует не только большего времени расчёта, но и в три раза большего объёма памяти для хранения коэффициентов переноса излучения отдельно для каждого цветового канала.
После моделирования распространения света вся информация записывается в файл, который потом может прочитать рисующие данную сцену приложение.
Мы рассмотрели программу расчёта коэффициентов переноса излучения в случае использования вершинных шейдеров. То есть, коэффициенты находятся для всех вершин треугольников, составляющих сцену. Для случая пиксельных шейдеров программа почти что аналогична, только дополнительно указывается размер текстуры, в которую будут записываться коэффициенты. Чем больше размер текстуры, тем выше визуальное качество изображения, но больше время расчёта и больший объём данных придётся хранить. Причём, с ростом разрешения текстуры с 256 до 512, например, количество данных возрастает в 4 раза. Косвенно, это может сказываться и на скорости отрисовки, поскольку потребует большей пропускной способности видео памяти.
Сжатие массива коэффициентов
С точки зрения сегодняшних видео акселераторов, значительным ограничением метода является большой объём хранимой информации и длинные вычисления на этапе рендеренга. Например, если используются 36 базисных сферических функций и 3 цветовых канала, то в случае использования пиксельных шейдеров необходимо хранить в каждом текселе 108 коэффициентов, желательно, float. Мало того, что это просто съест всю память видео ускорителя, такие длинные шейдеры из более чем полусотни сложных команд (для ускорения используются, естественно, векторные команды для операций с четвёрками чисел) будут неподъёмными даже для новейших VPU. Но и это ещё не всё, DirectX9 накладывает ограничения на длину шейдеров и количество констант, и эти сложные шейдеры в них не вписываются. И вот для обхода всех вышеперечисленных препятствий используется сжатие массива коэффициентов переноса излучения.
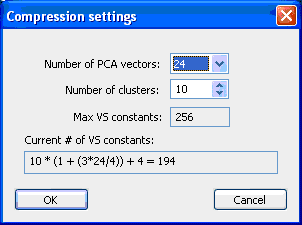
Напомню, в шейдере происходит вычисление выражения
Запишем его в векторной форме
где L и F n-мерные векторы. N - количество базисных сферических функций. Идея сжатия такова: проанализируем массив коэффициентов F, - это гигантский массив, в котором содержится информация об освещённости в каждой точке сцены, и выберем M<N векторов B1, ..., Bm, линейные комбинации которых наилучшим образом приближают вектора F. Тогда запишем для каждой точки x вектор F(x) в виде
Теперь можно записать выражение (L,F(x)), которое надо вычислить в шейдере, как (L,W1(x)*B1+…+Wm(x)*Bm)=W1(x)*(L,B1)+...+Wm(x)*(L,Bm). Вектора Bm постоянны для всех точек, как и вектор коэффициентов разложения внешнего света L, так что скалярные произведения ai=(L,Bi) считаются один раз. И, таким образом, в шейдере остаётся вычислить (W,a), и хранить нужно только M коэффициентов W(x). Так как M взято меньше N, достигается значительная экономия всех ресурсов.
Алгоритм сжатия работает достаточно хорошо, тем более, что данные не случайные, а меняются достаточно непрерывно от точки к точки.
Имплементация
Рассмотрим теперь особенности метода применительно к реальным игровым приложениям. Самым главным ограничением является, естественно, невозможность изменения взаимного положения объектов сцены. Поскольку коэффициенты распространения света внутри сцены зависят только от относительного положения объектов, сцену можно только целиком вращать или уменьшать или увеличивать. При таких преобразованиях сохраняется относительное положение частей сцены. Не то, что бы это совсем плохо, поскольку в практически всех современных трёхмерных играх сцена, из-за того же предварительно расчёта освещённости, и так статична, кроме некоторого количества движущихся моделей. Но при динамическом освещении сцены придётся динамически вычислять тени и от всех движущихся моделей, а их заранее не рассчитаешь. Однако, не все методы рисования динамических теней хорошо совмещаются с данным методом освещения всей сцены. Данный метод предполагает реалистично размытые тени, а метод стенсил-буфера позволяет рисовать достаточно чёткие резкие тени. Так что придётся использовать проективные текстуры с размытым теневым силуэтом. А их применение имеет свои ограничения.
Второй серьёзный минус заключается в ограничении на положение источников света вне сцены. Это обусловлено аппроксимацией исключительно внешнего входящего в сцену света. Таким образом, можно расположить светильник за окнами некоторой комнаты, но внутри под потолком повесить нельзя. Можно разбить сцену на отдельные подмодели, и отдельно для каждой из них рассчитать освещение. Но в этом случае придётся как-то совмещать различные карты освещённости на стыках между составляющими сцену подмоделями. С одной стороны, из-за приближённого характера расчёта освещения даже в общих точках различных подмоделей оно будет отличаться. Но, поскольку тени предполагаются очень размытыми, освещение можно попытаться как-то сгладить в местах совмещения подмоделей для улучшения визуального качества изображения.
Таким образом, метод хорошо подходит для отображения освещения от источников света типа солнца, которые светят из окон. Другое использование потребует дополнения метода и каких-то трюков. Можно ещё освещать льющимся с неба светом открытые пространства, но это потребует очень большого объёма хранимых данных, поскольку очень велика площадь поверхности сцены.
Видео ускоритель для PRT
Рассмотрим теперь основные требования метода к VPU. Использование вертексного варианта требует очень высокой степени тесселяции сцены. Всё должно быть разбито на маленькие треугольники. Там, где была плоская поверхность, представленная несколькими большими треугольниками, должно стать море мелких треугольников. Иначе будут проявляться артефакты расчёта теней. Они будут очень грубыми и неправильной формы. Дополнительных данных для каждой вершины нужно не очень много, так что на первый план выходит "вершинная" производительность.
Поскольку шейдер освещения довольно прост, там нет ни циклов, ничего такого, просто "в лоб" - сумма произведений, этот вариант требует всего лишь вершинных шейдеров версии 1.1, которые поддерживаются большим количеством не самых новых ускорителей. Это позволит разработчикам гипотетической игры, использующей данную технологию, не ждать распространения DirectX9 ускорителей, чтобы не ограничивать множество покупателей.
Использование пиксельных шейдеров позволяет достичь существенно лучшего качества изображения, особенно, в высоких разрешениях, но и требует значительно больших ресурсов. В первую очередь, производительности пиксельных шейдеров, поскольку, как не сжимай массив коэффициентов, всё равно шейдер остаётся достаточно длинным. Правда, так как в данном случае информация хранится в текстуре, и она более детальна, чем вершинная, то можно сильнее сжать массив коэффициентов. Потери от сжатия компенсируются большим количеством информации по сравнению с вертексным способом. Это позволит уложиться в более строгие ограничения на длину и количество констант для пиксельных шейдеров.
Пиксельный вариант требует текстуры достаточно большого размера, каждый элемент такой текстуры хранит более десяти коэффициентов, так что будет чем заполнить видео память. Для сложной сцены потребуется (10 текстур 1024х1024х32bit) сотни мегабайт текстур. Соответственно, требования к пропускной способности памяти серьёзно возрастут.
Как ни крути, качественная реализация нового метода затенения позволит полностью загрузить самую мощную видеокарту. Не будет такого, чтобы видео ускоритель простаивал в ожидании процессора. Использование пиксельных шейдеров так особенно, они и так сейчас совсем не быстро выполняются на новых ускорителях среднего уровня. Кстати, и места на жёстком диске потребуется уйма. Ведь для каждого уровня необходимо хранить сотни мегабайт предварительно рассчитанных данных...
Заключение
В заключении можно с радостью отметить то факт, что развитие игровой графики идёт не только экстенсивными путями эксплуатации мощности новых VPU, но появляются принципиально новые алгоритмы решения важных задач. И это должно разнообразить наскучивший уже вид современных трёхмерных игр.
Использованные материалы
Для желающих более детально ознакомиться с технологией, привожу ссылки на первоисточники.
DirectX9.0 SDK (Summer update)
Sloan, Peter-Pike, Jan Kautz, and John Snyder. "Precomputed Radiance Transfer for Real-Time Rendering in Dynamic, Low-Frequency Lighting Environments" . ACM Transactions on Graphics (TOG), Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH), pp. 527-536. New York, NY: ACM Press, 2002.
Sloan, Peter-Pike, Jesse Hall, John Hart, and John Snyder. "Clustered Principal Components for Precomputed Radiance Transfer" . ACM Transactions on Graphics (TOG), Vol. 22, Issue 3 (SIGGRAPH), pp. 382-391. New York, NY: ACM Press, July 2003.
Green, Robin. "Spherical Harmonic Lighting: The Gritty Details" . Game Developers Conference, San Jose, CA, March 2003.




