Ваш город: Москва
Как компьютер рассчитывает изображения. Технологии программного рендеринга

Perry Harovas, mray3.2
Эпиграф: "We do not expect to be able to display the object exactly as it would appear
in reality, with texture, overcast shadows, etc. We hope only to display an
image that approximates the real object closely enough to provide a certain
degree of realism."
B. T. Phong
Введение
Истина одна, но пути ее достижения могут быть самыми разными.
Эта мысль как нельзя более справедлива в отношении рассматриваемой темы – компьютерных алгоритмов расчета освещенности трехмерных искусственных (синтезированных на компьютере, или просто – синтетических) сцен. Поскольку они, эти самые алгоритмы, изначально появились как абсолютная фикция, имеющая очень мало общего с физикой реального мира. Единственное требование, которое к ним предъявлялось – полное или очень близкое соответствие рассчитанных изображений с реальным миром. Ну да, та самая пресловутая фотореалистичность. Однако, одного этого требования оказалось достаточно, чтобы изначально фиктивные методы эволюционировали в почти физически корректные модели описания динамики света. История этой эволюции – это история роста производительности электронных вычислительных машин и создания эффективных алгоритмов расчета освещенности. Я предлагаю Вам совершить экскурс по основным этапам этой захватывающей истории и познакомиться с ее основными этапами. Такое путешествие имеет также и вполне прагматическую ценность (я на это надеюсь :)) – многие из созданных моделей и алгоритмов расчета освещенности используются и поныне, поэтому их изучение должно стать основой осмысленного мастерства всех, кто имеет дело с графическим моделированием реального мира при помощи компьютера.
Глава 1. Локальная модель освещения (local Illuminating model)
В соответствии с принятым в компьютерной графике подходом, расчет освещенности распадается на две основные задачи. Первая – определить способ расчета освещенности в произвольной точке трехмерного пространства, решается при помощи построения обобщенной математической модели освещенности (Illuminating model). Вторая задача –применение Illuminating model для компьютерных расчетов освещенности трехмерных объектов с конкретной геометрией и свойствами поверхности, решается при помощи так называемой модели затенения (Shading model).
Моделей освещенности к настоящему моменту разработано несколько. Самая первая, и самая простая – локальная модель освещенности. Эта модель не рассматривает процессы светового взаимодействия объектов сцены между собой, а только расчет освещенности самих объектов. Вторая, глобальная модель освещенности – Global Illuminations, рассматривает трехмерную сцену как единую систему и пытается описывать освещение с учетом взаимного влияния объектов. В рамках этой модели рассматриваются такие вопросы, как многократное отражение и преломление света (ray tracing), рассеянное освещение (radiosity), caustic и subsurface scattering (photon mapping) и другие.
Начнем с самой простой модели освещенности, тем более что она и по сей день является главным способом расчета в рендерах scan-line типа (например, scan-line рендер 3ds max или mental ray).
В рамках локальной модели освещения рассматривается свет только от явных точечных источников света трех типов – omni, spot и directional, а само взаимодействие ограничивается только однократным отражением света от непрозрачной поверхности. Изображение формируется в результате отражения падающего на поверхность объектов света, интенсивность и цвет которого и необходимо рассчитать.
В самом общем случае, в свете требования фотореалистичности, эта модель должна также учитывать и неявное ambient-освещение. Ambient-освещение, или его еще называют фоновым (background), – это окружающее объект освещение от удаленных источников, чье положение и характеристики не известны. Необходимость учета ambient-освещения, пусть и очень грубо, обусловлена тем, что его вклад может быть достаточно велик – до 50% от общей освещенности. В Local Illumination считают, что фоновое освещение задает цвет (и его интенсивность) объекта в отсутствии явных источников света или в тени. Не несет никакой информации об объекте, кроме значения простого цвета, равномерно заливающего контур объекта.
Интенсивность такого освещения постоянна и равномерно распределена во всем пространстве, расчет его отражения поверхностью выполняется по формуле:
где

Увидеть этот тип освещения в "чистом виде" в 3ds max можно либо включив в настройках источника света свойство ambient only, либо изменив цвет Ambient Light панели Environment c черного (черный означает отсутствие окружающего освещения, принят по умолчанию) на более светлый и отключив diffuse/specular/ambient освещение в настройках источника света . В обычной ситуации, если цвет Ambient light в Environment отличен от черного (0, 0, 0 в RGB), свойство материалов Ambient color начинает оказывать влияние на цвет объекта – то есть max считает, что в сцене присутствует фоновое освещение, и начинает его просчитывать для поверхностей.

Объектам назначены материалы, абсолютно одинаковые, за исключением значения ambient color. При отключенном фоновом освещении они и выглядят одинаково.

Включение фонового освещения в Environment проявляет различие в ambient характеристиках этих материалов.
Часть света от прямых источников зеркально отражается поверхностью, а остальной свет диффузно рассеивается во всех направлениях. Кроме чисто зеркального отражения, которое имеют идеально отполированные поверхности, различают так называемое glossiness или распределенное зеркальное отражение – отражение в некотором створе углов, а не на один единственный угол. Такое рассеяние света обусловлено микрорельефом ("шероховатостью") поверхности, то есть поверхность реальных объектов не является идеально гладкой, а состоит из большого количества микровыступов и впадин, которые зеркально отражают падающий свет под разными углами. Результатом glossy-отражения является specular highlight – яркий световой блик, имеющий размер в зависимости от степени шероховатости поверхности.
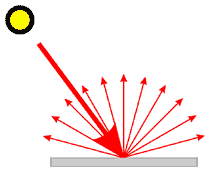
Диффузное рассеяние. Свет отражается равномерно под всеми углами.
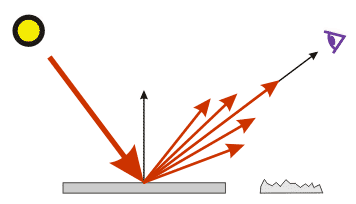
Зеркальное отражение под одним идеальным углом и glossy отражение в створе углов, обусловленное шероховатостью поверхности.
Интенсивность рассеянного света зависит от угла падающего на поверхность света по закону Ламберта (Lambert):
где
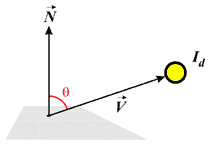
Другими словами, поверхность будет освещена больше, если свет падает на нее перпендикулярно
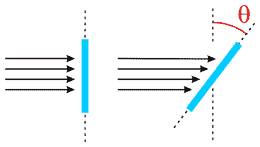
Диффузно рассеянный свет является главным источником визуальной информации о геометрии трехмерных объектов.

В 3ds max диффузное отражение света можно увидеть, отключив Specular в свойствах источников света. Второй способ достичь того же результата – установить черный цвет для Specular в свойствах материала и Ambient light панели Environment. Полностью отключить диффузное отражение света для поверхности можно назначив черный цвет свойству материала Diffuse.
Как мы уже обсуждали, свет отражается зеркально в некотором створе углов, и для большинства реальных материалов мы всегда видим зеркальную подсветку в форме светового пятна, а не в форме яркой точки. Поэтому, для расчета интенсивности зеркально отраженного света используется формула, предложенная Фонгом:
где
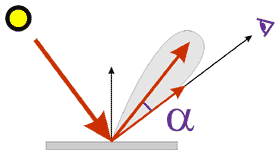
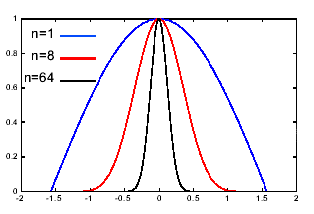
Формула Фонга – пример компьютерной фикции, поскольку она не имеет физического смысла. Ее используют просто потому, что она дает хорошие практические результаты.

Зеркальную подсветку в 3ds max можно увидеть, установив черный цвет Diffuse color материала и Ambient light панели Environment, либо включив только Specular в свойствах источников света. Для создания идеальной зеркально отражающей поверхности в свойствах материала необходимо полностью отключить диффузное отражение и ambient-цвет.

В 3ds max коэффициенту
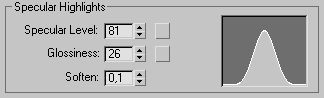
Наконец, чтобы различать объекты, находящиеся на разных расстояниях от камеры, используется функция затухания интенсивности света с расстоянием:
В компьютерной графике используется модифицированная формула, более приемлемая на практике:
Таким образом, локальная модель освещенности предполагает расчет отраженной фоновой освещенности, диффузного и зеркального отражения от прямых источников:




Эта формула для расчета освещенности по одному каналу для одного источника света. Полная освещенность должна рассчитываться по всем трем основным каналам (RGB) и для всех источников освещения в трехмерной сцене и затем суммироваться. Эта модель получила название модели освещенности Фонга (не путать с моделью затенения Фонга, об этом ниже), по имени автора ее разработавшего. Является основной моделью в скан-лайн рендерах.
Как видите, локальная модель освещенности довольно проста. Проста настолько, что обсуждать ее достоинства и недостатки бессмысленно, она дает неплохие практические результаты – на том и остановимся.
Глава 2. Модели затенения (Flat, Gauround, Phong и другие)
Если бы мы могли применять модель освещенности для расчетов в каждой точке поверхности, необходимость в создании моделей затенения попросту не возникла. Однако, такой расчет очень расточителен в отношении вычислительных ресурсов компьютерной системы и потому неприемлем. На практике расчет освещенности выполняется не для всех точек поверхности, а лишь для некоторых из них. Задача моделей затенения (shading) состоит в том, чтобы "правильно" определить эти точки и аппроксимировать результат "честных" вычислений модели освещения в этих точках на всю поверхность с соблюдением принципа фотореалистичности.
Самая первая и самая быстрая модель затенения, разработанная в компьютерной графике – Flat shading, в настоящее время мало используется и имеет скорее историческое значение.
Суть Flat-затенения состоит в том, что освещенность рассчитывается только для одной точки полигона, и затем рассчитанное значение просто присваивается всему полигону (всем точкам полигона). Более точно, для каждого полигона поверхности рассчитывается нормаль, с помощью которой и вычисляется общая для одного полигона освещенность. Таким образом, цвет в пределах одного полигона неизменен и резко меняется на границах между разными полигонами, в результате чего трехмерная поверхность приобретает типичный "граненый" вид.
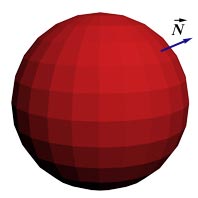
Освещенность по модели затенения Flat
При увеличении количества полигонов, образующих поверхность, а также – при большом удалении трехмерного объекта от камеры и источников света, эта модель затенения может давать вполне фотореалистичные результаты.
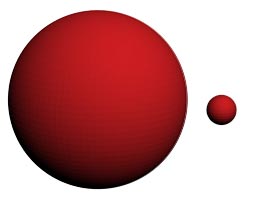
С этой моделью затенения связан интересный визуальный артефакт, известный как Mach band effect – на границе скачкообразного перехода интенсивности человек видит темные цвета более темными, а светлые цвета более светлыми, чем они есть на самом деле, что в нашем случае еще более усиливает эффект "гранености" поверхности.
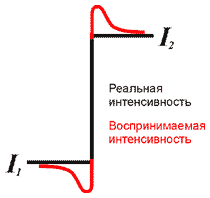
Mach band effect
Модель затенения Гуро (автор – Henry Gauround, модель разработана в 1971 году).
В этой модели освещенность рассчитывается для каждой вершины полигона, а полученный цвет интерполируется сначала вдоль границ полигона и затем – для внутренних точек. Для расчета освещенности вершины используется нормаль, получаемая усреднением нормалей всех полигонов, для которых данная вершина является общей.
Расчет достаточно быстр, дает сглаженные цветовые переходы на всей поверхности и позволяет вычислять зеркальные подсветки.

Расчет освещенности по Гуро

Получение нормали вершины: нормали всех полигонов, содержащих вершину, складываются по правилам векторного сложения, и результат делится на сумму длин векторов нормалей полигонов (нормализация – вектор вершины должен быть единичной длины).
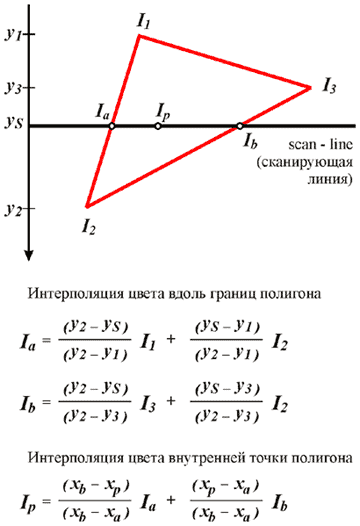
Вариант интерполяция цвета вершин в пределах полигона вдоль
направления сканирующей линии (сверху вниз)
Основным достоинством затенения по Гуро является сглаженность цветовых переходов при высокой скорости вычислений. Последнее обстоятельство обусловило широкое применение этой модели в приложениях реального времени, например – эта модель принята по умолчанию в OpenGL. Видовые окна 3ds max, Maya и других программ 3d моделирования также отображают объекты с применением затенения Гуро.
Но эта модель имеет и ряд серьезных недостатков, главным среди которых является неверное отображение подсветок, особенно если поверхность низкополигонная. Во-первых, подсветки имеют "звездообразную" форму и часто визуально проявляют полигональную структуру поверхности. Во-вторых, подсветки просто-напросто могут внезапно исчезать, если попадают на внутреннюю точку полигона и т.д. Понаблюдать за этими явлениями можно в видовом окне 3ds max, вращая низкополигонную сферу. Второй существенный недостаток – зависимость результата интерполяции от поворотов. Причина тому – в интерполяции цвета вдоль сканирующей линии, при повороте полигона относительно которой расчет цвета одного и того же пиксела осуществляется с использованием разных границ полигона. Кроме того, в модели затенения по Гуро также может проявляться Mach band effect, хоть и в меньшей степени, а также имеются проблемы с перспективой.
Затенение по Фонгу (автор - Phong Biu-Thuong, модель разработана в 1975 году).
Модель затенения по Фонгу вычисляет с помощью локальной модели освещенности интенсивность для каждого пиксела поверхности. Для этого, как и в модели Гуро, находятся нормали всех вершин полигона, затем эти нормали интерполируются вдоль границ полигона и для внутренних точек полигона – вдоль сканирующей линии, подобно тому как интерполировалась интенсивность освещения в модели Гуро. И уже затем для каждого пиксела полигона рассчитывается освещенность.

Затенение по Фонгу. Хорошо заметна несглаженная полигонная
структура геометрии по контуру объекта
Интерполяция нормалей вместо интенсивностей разом решает вопрос с подсветками – поскольку теперь известна нормаль в каждой точке поверхности, интенсивность можно рассчитать точно. Знание нормали в каждой точке поверхности позволяет применять к поверхности bump-mapping при помощи растровой карты, описывающей "отклонения" нормалей в точках. Рассчитанные при помощи модели затенения Фонга нормали высокополигонной модели можно сохранить как специальную растровую карту (карту нормалей) и затем накладывать ее на низкополигонную модель – присваивать каждому пикселу низкополигонной модели нормаль, рассчитанную на высокополигонной модели. В результате, рендер низкополигонной модели будет почти таким же качественным, как и рендер высокополигонной модели. Кстати, заслуживающие доверия источники утверждают, что данная технология будет очень широко использоваться в Half-Life 2 и Doom 3.
Недостатки:
Медленный расчет
Полигонные силуэты по контуру объекта
Зависимость от ориентации
Проблемы с перспективой.
Существуют разновидности модели затенения по Фонгу: Blinn, Cook-Torrance и Ward (anisotropic).
Модель затенения Blinn несколько видоизменяет размер зеркальной подсветки в зависимости не только от направления на источник света, но и от направления на наблюдателя. Чем меньше угол между поверхностью и направлением на наблюдателя, тем больше размер подсветки, поскольку поверхность сильнее разбрасывает свет.
Модель затенения Cook-Torrance является логичным развитием модели Blinn, делая подсветку зависящей еще и от длины волны. Эта модель позволяет получать дополнительные цветовые переходы на краях подсветки для шероховатых металлических и пластиковых материалов.
Модель затенения Ward (anisotropic shading) позволяет определять преимущественное направление шероховатостей поверхности и изменять форму подсветки в зависимости от такого направления.

Анизотропная модель затенения
Что касается теней, то поскольку локальная модель освещенности не рассматривает взаимодействие объектов между собой, тени просчитываются при помощи некоторых искусственных процедур. Например, рендер генерирует растровое изображение (теневую карту, shadow map) объекта и затем проектирует ее по направлению от источника к объекту. Такие тени не могут учитывать цвет, прозрачность и другие сложные свойства объектов. Полноценный расчет теней возможен только начиная с рейтресинга.
Глава 3. Классический Ray Tracing
Готовы? Поехали!
Классический ray tracing, или метод трассировки лучей, предложен Артуром Аппелем (Arthur Appel) еще аж в 1968 году и дополнен алгоритмом общей рекурсии, разработанным Whitted в 1980 году. Понадобилось почти 12 лет эволюции вычислительных систем, прежде чем этот алгоритм стал доступен для широкого применения в практических приложениях.
Суть метода заключается в отслеживании траекторий лучей и расчета взаимодействий с лежащими на траекториях объектами, от момента испускания лучей источником света до момента попадания в камеру. Под взаимодействием луча с объектами понимаются процессы диффузного (в смысле модели локальной освещенности), многократного зеркального отражения от их поверхности и прохождение лучей сквозь прозрачные объекты. Таким образом, ray tracing – первый метод расчета глобального освещения, рассматривающий освещение, затенение (расчет тени), многократные отражения и преломления. Различают два основных вида метода трассировки лучей: прямой – forward ray tracing, и обратный – backward ray tracing. Сразу оговорюсь, ray tracing вообще не использует модели шейдинга, по определению. Расчет освещенности "честно" выполняется во всех точках пересечения лучей и объектов.
В forward ray tracing траектории лучей строятся от источника ко всем точкам всех объектов сцены (первичные лучи). Затем проверяется ориентация каждой точки относительно источника, и, если она лежит на стороне объекта, обращенной в противоположную от источника сторону, точка из расчетов освещенности исключается. Для всех остальных точек вычисляется освещенность с помощью локальной модели освещения. Если объект не является отражающим или прозрачным, то есть поверхность объекта только диффузно рассеивает свет, траектория луча на этой точке обрывается (заканчивается). Если же поверхность объекта обладает свойством отражения (reflection) и/или преломления (refraction), из точки строятся новые лучи, направления которых совершенно точно определяются законами отражения и преломления.
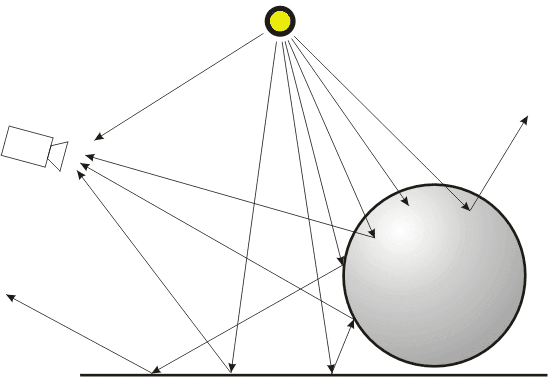
Прямая трассировка лучей. Лучи должны быть построены от каждого источника освещения ко всем точкам поверхностей всех объектов сцены и отслежены в соответствии с законами отражения и преломления.
Для построенных таким образом траекторий новых лучей может быть только три исхода. Луч либо выходит за пределы видимой из камеры области сцены, в этом случае все проделанные для него до этого момента расчеты освещенности отбрасываются, поскольку они не принимают участия в формировании изображения. Или луч попадает в камеру, тогда рассчитанная освещенность формирует цвет соответствующего пиксела изображения. Или луч встречает на своем пути новый объект, тогда для новой точки пересечения повторяется расчет освещенности и построения лучей отражения и преломления в зависимости от свойств поверхности объекта (рекурсия). Построение новых траекторий и расчеты ведутся до тех пор, пока все лучи либо попадут в камеру, либо выйдут за пределы видимой области. Очевидно, что при прямой трассировке лучей мы вынуждены выполнять расчеты для лучей, которые не попадут в камеру, то есть, проделывать бесполезную работу (вот-вот, именно это и называется "грузить", в данном случае – процессор :)). По некоторым оценочным данным доля таких "слепых" лучей довольно велика. Эта главная, хотя и далеко не единственная, причина того, что метод прямой трассировки лучей считается неэффективным и на практике не используется (ну и зачем Вы все это читали?! :).
Второй метод – обратной трассировки лучей, или backward ray tracing. Этот метод расчетов основывается на построении лучей от наблюдателя через плоскость экрана вглубь сцены, а не от источника, то есть – наоборот. Забегая вперед скажу, что это очень изящный способ решить массу проблем, возникающих при прямой трассировке, а сам метод отличается простотой и понятностью.
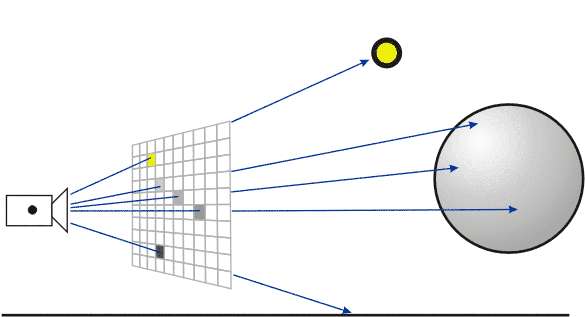
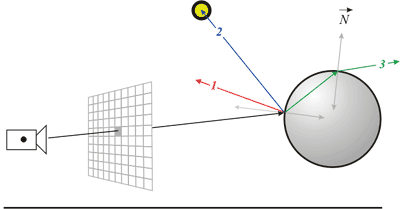
Схема расположения наблюдателя и трехмерной сцены для метода обратной трассировки лучей. Луч строится от наблюдателя через видовое окно до первого пересечения с объектом и далее – в соответствии с законами преломления и отражения.
Лучи теперь строятся иначе. А именно, по двум точкам: первая точка, общая для всех лучей – положение камеры (наблюдателя), вторая точка определяется положением пикселя на плоскости видового окна. Таким образом, направление каждого луча строго определено (две точки в пространстве определяют одну и только одну прямую – школьный курс геометрии), и количество первичных лучей также известно – это общее количество пикселей видового окна. Например, если видовое окно имеет 800 пикселей по ширине и 600 пикселей по высоте, количество лучей составит 800х600= 480 000. И это только начало.
Каждый луч вдоль заданного направления продляется от наблюдателя вглубь трехмерной сцены, и для каждой траектории выполняется проверка на пересечение со всеми объектами сцены и с отсекающими плоскостями. Если пересечений с объектами нет, а есть пересечение только с плоскостью отсечения, значит луч выходит за пределы видимой части сцены, и соответствующему пикселю видового окна присваивается цвет фона. Если луч пересекается с объектами сцены, то среди всех объектов выбирается тот, который ближе всего к наблюдателю. В точке пересечения с таким объектом строится три новых, так называемых вторичных луча.
В точке пересечения луча с объектом строится три вторичных луча – один в направлении отражения (1), второй – в направлении источника света (2), третий в направлении преломления прозрачной поверхностью (3).
Один луч строится в направлении источника света. Если источников несколько, строится несколько таких лучей, по одному на каждый источник. Основное назначение этого луча – определить ориентацию точки (обращена точка к источнику или от него), наличие объектов, закрывающих точку от источника света, и расстояние до источника света. Если точка обращена в противоположную сторону от источника света или закрыта другим непрозрачным объектом, освещенность от такого источника не рассчитывается, точка находится в тени. В случае затеняющего прозрачного объекта интенсивность освещения уменьшается в соответствии со степенью прозрачности. Если точка закрыта от освещения всеми источниками сцены, ей присваивается фоновый ambient цвет. В противном случае точка освещена, интенсивность и цвет освещения рассчитываются при помощи локальной модели освещенности (diffuse + specular) как сумма освещенностей от всех источников, для которых эта точка не закрыта другими объектами. Этот тип луча получил название shadow ray (иногда его еще называют illumination ray) – теневой луч. Если поверхность объекта не является отражающей и непрозрачна, теневой луч – единственный тип лучей который строится, траектория первичного луча обрывается (заканчивается), и дальнейшие расчеты не выполняются. Рассчитанный цвет (освещенности или тени) присваивается тому пикселю видового окна, через который проходит соответствующий первичный луч.
Второй луч строится, если поверхность объекта обладает отражающими свойствами, и называется reflection ray, или луч отражения. Направление отраженного луча определяется по закону:
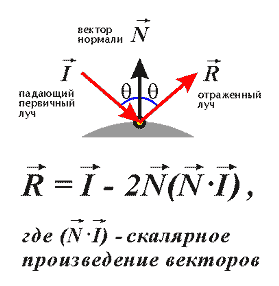
Эта формула используется для определения направления отраженного луча.
Для отраженного луча проверяется возможность пересечения с другими объектами сцены. Если пересечений нет, то интенсивность и цвет отраженного луча равна интенсивности и цвету фона. Если пересечение есть, то в новой точке снова строится три типа лучей – теневые, отражения и преломления.
Третий луч строится, если поверхность объекта прозрачна, и носит название transparency ray, т.е. луч прозрачности. Направление для преломленного луча определяется следующим образом:
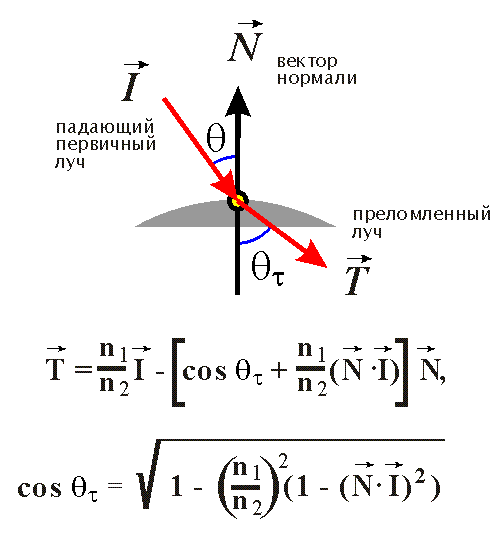
Эти формулы используются для определения направления преломленного луча.
n1 и n2 – коэффициенты рефракции для первой среды (в которой распространяется первичный луч) и второй среды прозрачного объекта. Так же, как и в предыдущем случае, проверяется пересечение вновь построенного луча с объектами, и, если они есть, в новой точке строятся три луча, если нет – используется интенсивность и цвет фона.
Таким образом, для каждого первичного луча можно построить древовидную структуру следующего вида:
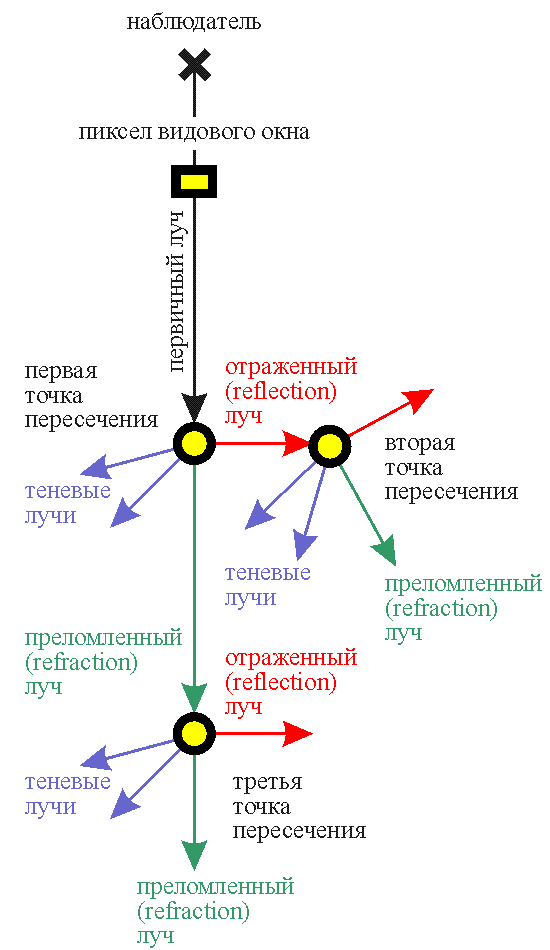
В каждой точке пересечения теневые лучи строятся всегда. Преломленный и отраженный лучи строятся при условии, что поверхность пересечения обладает свойствами отражения или преломления. Если объект такими свойствами не обладает, в точке пересечения вычисляется освещенность (diffuse и specular), и луч обрывается (считается, что он заканчивается на источнике света). В идеале, процесс продолжается до тех пор, пока все лучи либо не будут рассеяны на чисто диффузных поверхностях, либо не выйдут за пределы видимой области.
Если древовидная структура для данного луча построена, то расчет освещенности можно выполнить в следующем порядке. Для каждой ветви дерева спускаемся вдоль древовидной структуры к последнему пересечению вторичного луча и поверхности (будем дальше называть их узлами). Поскольку это последний узел в цепи, вкладов от преломлений и отражений нет. Поэтому освещенность узла вычисляется при помощи локальной модели освещения с учетом видимости источников света для данного узла. Затем, вычисленная освещенность передается вверх по ветви к следующему ближайшему узлу. Освещенность в этом узле будет вычисляться по формуле:
где
Таким образом, результаты освещенности накапливаются при подъеме от самого последнего узла через все узлы ветви и для всех ветвей одного пиксела видового окна. Изображение можно считать построенным, когда цвета всех пикселов видового окна (все соответствующие деревья для каждого первичного луча) вычислены.
Насколько глубоким может быть дерево узлов? Как далеко прослеживаются вторичные лучи?
Естественным завершением трассировки лучей является выход всех испущенных вторичных лучей за пределы видимой области и их рассеяние на чисто диффузных объектах. Результат вычислений будет наиболее точным. Но, если сцена достаточно сложна, такой расчет будет очень медленным, а в некоторых случаях и невозможным по причине ограниченности аппаратных ресурсов. Легко увидеть, что вклад освещенности от каждого нового вторичного луча очень быстро уменьшается по той простой причине, что коэффициенты свойств отражения и преломления материалов меньше единицы. Например, если коэффициент отражения
Основные достоинства рекурсивного метода обратной трассировки лучей – расчет теней, многократных отражений и преломлений, значительно повысивших степень реалистичности компьютерных рендеров.
Основные недостатки: неучет вторичного освещения от диффузно отраженного объектами света; низкая скорость и высокая вычислительная стоимость расчетов – в классическом рейтресинге необходимо проверять на пересечение каждый луч со всеми объектами сцены, в результате от 70 до 95 процентов всего времени расчетов тратится на вычисление пересечений; резкие границы цветовых переходов тени/подсветок/прозрачности; aliasing – "зазубренность" линий и т.д.; дискретность определяющих цвет пиксела первичных лучей – одного первичного луча недостаточно для корректного определения цвета пиксела, формирующего изображение.
Глава 4. Distributed Ray Tracing (DRT), он же Stochastic Ray Tracing
Дальнейшая эволюция алгоритмов ray tracing протекала в направлении преодоления недостатков классического метода обратной рекурсивной трассировки лучей (далее – просто трассировки лучей). Так, для подавления эффекта aliasing и различных его проявлений, например – "зазубренных" линий, были разработаны различные методы сглаживания – supersampling, adaptive supersampling, stochastic и statistical sampling.
Вообще принцип вычисления усредненных величин, или получение окончательного цвета пиксела по нескольким промежуточным значениям, имеет гораздо более глубокий смысл, чем просто сглаживание. Испуская один первичный луч на пиксел, мы пытаемся описать дискретными величинами – вычисленными интенсивностями в отдельных точках пересечения лучей и объектов, диапазон непрерывных значений реальной освещенности. Если это и можно сделать корректно, то только при соблюдении определенных правил. Такие правила можно получить, например, из свойств зрения человека. А именно, зрительное восприятие человека основано на принципе интегрирования, или смешивания, цветов близко расположенных пространственных точек. Точнее, человек всегда зрительно воспринимает некоторую пространственную область, а не отдельные точки, и степень смешивания тем больше, чем дальше расположен зрительный объект. Представим себе две небольшие светящиеся лампочки, допустим, синюю и желтую, разнесенные на некоторое расстояние друг от друга. Чем дальше от них мы будем находиться, тем сложнее будет их различать как два отдельных объекта. На достаточно большом расстоянии они вообще сольются для нас в один объект, светящийся зеленым светом.
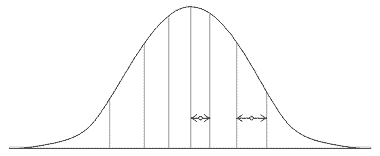
Поэтому, усреднение цвета пиксела по нескольким промежуточным значениям столь важно, и его использование дает не только сглаживание, но и повышает общее качество рендера, поскольку делает его естественным для нашего восприятия. Это объяснение носит качественный характер. Но существует и точная математическая теория сэмплинга, как операции представления непрерывных функций набором дискретных значений. Эта теория использует так называемый Фурье-анализ. Для нас важно то, что в рамках этой теории получено совершенно строгое правило, определяющее способ сэмплирования. Это правило – теорема Найквиста (Nyquist), и оно гласит, что для того чтобы набор дискретных значений (сэмплов) корректно описывал непрерывную функцию, частота сэмплирования должна быть как минимум в два раза больше максимальной частоты функции. Пример:
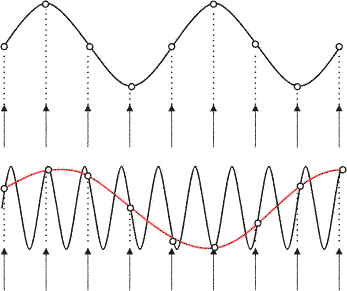
На верхнем рисунке частота сэмплирования синусоидальной функции больше частоты самой функции более чем в два раза, поэтому по сэмплам исходная функция может быть восстановлена правильно. На нижнем рисунке частота сэмплирования слишком мала, в результате сама функция по сэмплам правильно восстановлена быть не может. Получаемая по сэмплам новая функция, отмеченная красным цветом, значительно отличается от исходной.
Результат неверного сэмплирования – алиасинг. Пример пространственного алиасинга –ступеньки на границах объектов, временного алиасинга – вращение колес мчащегося на экране поезда в обратную сторону или "дерганое" воспроизведение видео и анимации, пример звукового алиасинга – появление поддельных звуков в оцифрованной дорожке, отсутствующих в аналоговом оригинале. Теорема Найквиста определяет нижнюю границу сэмплинга, и совершенно ясно, что чем выше частота сэмплирования, тем точнее и качественнее представление непрерывной функции.
В простом supersampling через каждый пиксел видового окна испускается не один, а несколько первичных лучей. Затем, вычисленные значения интенсивности первичных лучей в пределах одного пиксела усредняются. Этот простой метод сэмплинга дает на практике достаточно хорошие результаты, но ценой значительного увеличения времени расчетов.
Пример пропускания лучей через разные части пиксела для суперсэмплинга с девятью лучами.
По некоторым данным, для получения гарантированно качественных результатов, через пиксел должно быть испущено не менее 20 первичных лучей. То есть, для получения качественного anti-aliasing методом supersampling время расчетов увеличится в 20 раз! Вряд ли это можно считать приемлемым решением, тем более что вовсе не для всех пикселов изображения столь качественное сглаживание необходимо (на самом деле – только для граничных).
Идея адаптивного суперсэмплинга (adaptive supersampling) использует именно это соображение – первоначально через пиксел пропускается небольшое количество лучей, скажем – три. Вычисленные значения сравниваются между собой. Если разница не превышает заданную величину, количество лучей не увеличивается, а интенсивность усредняется. Если какой-либо из лучей существенно отличается от других, соответствующий субпиксел "простреливается" еще тремя лучами, и все повторяется.
Пример адаптивного сэмплинга.
Выход из цикла происходит либо после достижения равномерности интенсивностей лучей на уровне субпикселов (что не всегда может быть достигнуто), либо после заданного количества итераций. Таким образом, adaptive supersampling использует нужное количество лучей в зависимости от того, является или нет пиксел "пограничным" :).
Также интересен и тот факт, что фоторецепторы глаза распределены на сетчатке нерегулярно, а некоторым случайным образом – на разном расстоянии. Главное – существует минимальная дистанция, ближе которой рецепторы не располагаются. Именно такое строение фоторецепторов послужило идеей еще одного вида суперсэмплинга – stochastic supersampling. Этот метод разбивает пиксел на заданное количество субпикселов, скажем 4х4=16. Вычисляются координаты центров субпикселов, и затем к ним применяется небольшой шум – случайные отклонения по координатам x и y (jittering). Так что новые центры смещаются случайным образом в пределах субпикселов. Затем через них пропускают первичные лучи, которые теперь распространяются под случайными углами.

Пример стохастического сэмплинга.
Этот метод дает более качественные результаты, по сравнению с простым и адаптивным суперсэмплингом. Осталось поговорить о способе усреднения величин. Это тоже важно, поскольку также влияет на качество конечного изображения. Самый простой способ усреднения – сложить интенсивности и разделить их на количество лучей (box filter), используется довольно часто и дает неплохие результаты. В некоторых случаях гораздо точнее оказывается весовое или статистическое усреднение, когда вклад интенсивности определяется весовыми коэффициентами, значения которых задаются некоторой функцией. Например, это может быть хорошо известная функция статистического распределения Гаусса и другие.
Ну что же, пожалуй, теперь мы готовы поговорить о distribute ray tracing (далее иногда будем использовать аббревиатуру – DRT).
Основная идея distribute ray tracing была предложена Cook, Porter и Carpenter в 1984 году. В самом общем смысле ее суть состоит в том, что три типа вторичных лучей классического рейтресинга – теневой, зеркальный и прозрачности, должны "расщепляться" на несколько дополнительных лучей, распространяющихся в направлении "родительского" луча. Для каждого из расщепленных лучей находится значение освещенности, а освещенность в точке, откуда они были излучены, вычисляется как усредненное значение этих интенсивностей. По сути, вместо одного вторичного луча мы просто используем несколько и усредняем полученные значения интенсивности.
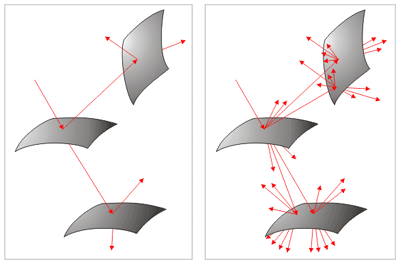
Схема на левом рисунке показывает диаграмму классического рекурсивного рейтресинга, схема на правом рисунке демонстрирует диаграмму distributed ray tracing. Как видим, основное отличие состоит в количестве трассируемых лучей – в DRT их гораздо больше.
На первый взгляд, увеличение числа лучей и усреднение интенсивностей не выглядит таким уж принципиальным новшеством. Тем не менее, удивительно, но факт – такое простое усовершенствование позволяет DRT просчитывать такие эффекты, как:
gloss (или scattered reflectance – размытые отражения)
translucency (размытая прозрачность)
penumbra (мягкая тень с размытыми краями)
depth of field (размывание объектов в зависимости от их положения относительно фокуса камеры)
motion blur (истинное размытие в движении)
Плюс стандартные возможности классического рейтресинга – тени, прозрачность и отражения – вот все это и делает DRT одним из основных алгоритмов расчета, применяемых в настоящее время.
Ключевым моментом расчетов освещенности методом DRT является расчет освещенности точки поверхности. Для этого DRT использует обобщенный метод расчета локальной освещенности, а именно, освещенность в некоторой точке поверхности x вычисляется при помощи интеграла следующего вида:
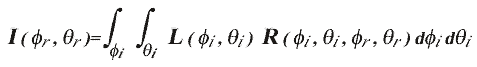
Интегрирование выполняется по полусфере единичного радиуса с центром в точке x и полюсом, выровненным относительно нормали поверхности в этой точке так, что нормаль проходит через полюс. Углы
Давайте немного посмотрим на то, что представляет собой этот интеграл.
Во-первых,
Во-вторых,
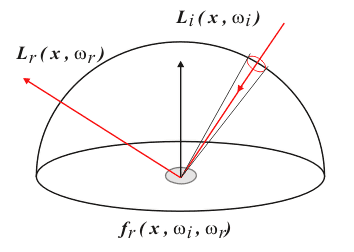
В-третьих, вычисляемая интегрированием интенсивность освещения в точке
Диффузное и зеркальное рассеяние локальной модели освещенности являются двумя частными случаями нашего интеграла. Модель освещенности DRT потому и является обобщением модели классического рекурсивного рейтресинга, что она позволяет рассчитывать отражение не только для идеально рассеивающих или идеально отражающих поверхностей, но и для поверхностей со свойствами, лежащими где-то между идеальными.
Так, теперь перейдем к вычислению интеграла. Несмотря на его устрашающий вид, расчет может быть выполнен не просто, а очень просто, если сделать несколько дополнительных допущений. А именно, в DRT, как я уже говорил выше, общая освещенность состоит из трех частей – от источника, отражения и преломления. DRT не рассматривает вторичных диффузных отражений света поверхностями объектов. Кроме того, в DRT считается, что интенсивность освещения в точке является простой суммой приходящих интенсивностей. То есть, наш интеграл можно представить в виде суммы трех интегралов: интеграла по источнику освещения, интеграла по отраженному свету и интеграла по преломленному свету. Все три интеграла можно рассчитать по отдельности и затем просто сложить результаты. Простое арифметическое сложение интенсивностей, кстати говоря, совершенно исключает из рассмотрения волновые свойства света, в частности, такие явления как дифракция и интерференция. Но это к слову, давайте продолжим с вычислениями.
В DRT, как и в классическом рекурсивном рейтресинге, необходимо строить диаграммы лучей для прослеживания отражений и преломлений. То есть, первичный луч выходит из пиксела видового окна, пересекается с ближайшей поверхностью, и, если она обладает свойствами отражения и прозрачна, из точки строятся вторичные лучи в направлении зеркального (идеального) отражения, в направлении идеального преломления и в направлении источников прямого освещения (вообще, направления распространения отраженного и преломленного луча определяются BDRF поверхностей). Для новых лучей находятся новые точки пересечения со следующими поверхностями, и процесс продолжается рекурсивно, как и в обычном рейтресинге, до того момента, когда луч в конце концов не достигнет поверхности, которая абсолютно не отражает и полностью непрозрачна. Будем называть всю диаграмму лучей деревом; первую точку пересечения первичного луча – корнем дерева; точки пересечения лучей и поверхностей – узлами; точку, на которой луч заканчивает путь – последним узлом ветви, а лучи от данного промежуточного узла до последнего узла – ветвью. Фф-у!
При вычислении освещенности для каждого первичного луча пиксела изображения сначала строится полная диаграмма лучей, до всех последних узлов всех ветвей. Затем спускаемся до одного из последних узлов какой-либо ветви. Поскольку узел последний, интеграл освещенности содержит только интеграл по прямому источнику освещения. Вычисляем его, получаем новую функцию распределения освещенности как результат отражения освещения поверхностью в точке узла. Эта функция должна быть передана вверх по ветви к предыдущему узлу. Если это ветвь, полученная в результате трассировки отраженного освещения, значит наша только что вычисленная интенсивность должна быть подставлена в интеграл отраженного освещения как функция описывающая приходящую освещенность. Если ветвь была получена трассировкой преломления, рассчитанная интенсивность подставляется как функция освещения в интеграл преломленного света. Теперь вычисляем интенсивность освещения в данном узле как сумму трех интегралов – описание источников освещения известно, описание распределения отраженного и преломленного освещения также известно благодаря вычислениям на предыдущем узле. Находим новую функцию распределения отраженного света в данном узле. Переходим к следующему. Так поднимаемся по всем узлам всех ветвей вверх – к корню дерева. Проделав вычисления для корневого узла и получив наконец
Вы думаете – это все!? Это только цветочки. А вот и ягодки. Дело осложняется тем, что точно вычислить интегралы в большинстве случаев невозможно.
Как быть?
Ну… я же обещал, что все будет просто. Ну так вот, точно интегралы никто и не считает. Вместо точного аналитического интегрирования пользуются численным методом нахождения значения интеграла, известным как метод Монте-Карло. Математический аппарат, стоящий за такими вычислениями, достаточно ужасен. Предлагаю поверить мне на слово, а кто не верит – вот Вам ссылочка на документ достаточно строго и полно рассматривающий метод Монте-Карло в применении к задачам компьютерной графики. Но предупреждаю – людям с неокрепшей психикой читать строго не рекомендуется!
Для нас важен чисто практический аспект этого метода. А именно, значение интеграла с той или иной величиной ошибки можно представить как сумму нескольких значений подынтегрального выражения с правильно подобранными множителями.
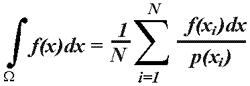
Другими словами, берем подынтегральное выражение, вычисляем его значение для нескольких значений переменных, складываем – и все! Ошибка будет тем меньше, чем больше значений вычисляется и суммируется. Кроме того правильно подобранный множитель p (
Поскольку BRDF известна заранее, трейсеры обычно предварительно просчитывают таблицы сэмплирования (lookup table) для каждой поверхности трехмерной сцены и сохраняют их для использования в нужный момент времени. Лично мое мнение – разумно предположить, что для сэмплирования лучше применять сочетание BDRF текущего узла и BDRF следующего узла ветви, поскольку они совместно определяют наиболее вероятные траектории переноса света между двумя конкретными узлами (поверхностями).
Правильный выбор направлений сэмплирования и весовых коэффициентов является "камнем преткновения" для современных рендеров, поскольку их оптимальное сочетание разом влияет и на качество рендера, и на скорость. Математически строгого решения пока нет, ведутся интенсивные исследования этого вопроса. А пока – либо быстро, либо хорошо, то есть, если программа-трейсер позволяет получить более качественный рендер за меньшее время, она должна считаться лучшей. Не суть, оставим решение этого вопроса, а также способ вычисления весовых коэффициентов p (
Итак, подведем некоторый промежуточный итог. Вычисление интегралов освещенности точек методом Монте-Карло приводит к появлению новых сэмплирующих лучей вместо вторичных лучей классического рекурсивного рейтресинга. Именно в этом и состоит смысл лучевой диаграммы, приведенной в начале главы. Достаточно интересно, что чисто математическая абстракция имеет в нашем случае и вполне конкретный физический смысл – лучи сэмплинга можно рассматривать как дополнительные траектории распространения света. Итак, каждый луч нашей диаграммы расщепляется на дополнительные лучи, для каждого из которых находятся точки пересечения, в каждой из которых испускаются новые сэмплирующие лучи… Количество лучей растет лавинообразно. Для ускорения расчетов, а также во избежание зацикливания трейсера на вычислении бесконечных траекторий (что вполне возможно) применяется Русская рулетка. Ничего общего с азартными играми – так называется математический метод отсечения ветвей рейтресинга, если их вклад становится меньше некоторой заданной величины.
Очевидно, что размывание преломления и отражения будет происходить тем больше, чем дальше расположены объекты друг от друга, и чем больше промежуточных преломлений и отражений происходит на пути к наблюдателю, поскольку все больше точек принимают участие в усреднении, и расположены они все дальше друг от друга – все как в жизни.

Размытые отражения. 3ds max 6, finalrender stage-1

Размытые отражения, еще один пример. 3ds max 6, finalrender stage-1

Размытые преломления. 3ds max 6, finalrender stage-1

Leonardo Cesar Veloso
С размыванием отражений и преломлений мы разобрались, а что насчет мягких теней? Мягкие тени в DRT получаются в результате вычисления видимости лучей, направленных на источник освещения. Основная трудность возникает при получении размытых теней от точечных источников. В DRT поступают так. Точечным считается только тот источник, который находится на большом расстоянии. Близко расположенные точечные источники заменяются сферой с небольшим радиусом. Далее, в направлении сферы испускаются сэмплирующие лучи. Если между точкой поверхности и источником света находится объект, то часть лучей может быть им закрыта, а часть лучей достигнет источника света.
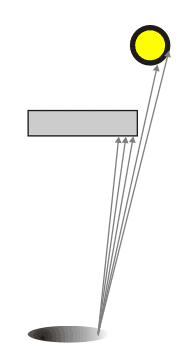
Сэмплирование источника света. Тень в точке вычисляется в зависимости от соотношения видимых и заблокированных лучей.
Поэтому освещенность точки вычисляется как интенсивность освещения, умноженная на отношение количества достигших источника лучей к общему количеству испущенных из точки лучей. Например, если из 16 лучей, первоначально испущенных из точки, только 4 достигают источника, то интенсивность освещения точки составит 4/16=1/4 от исходной, то есть уменьшится в 4 раза.

Penumbra (мягкая тень). 3ds max 6, finalrender stage-1
Нам осталось рассмотреть motion blur и depth of field.
Размытие в движении, или motion blur, получается в результате сэмплирования времени между кадрами. Берем два кадра, в которых есть движущийся объект. Время между кадрами делится на части (фракции), длительность каждой части немного отличается по случайному закону. Для каждой фракции просчитывается промежуточный кадр-изображение, затем все промежуточные кадры смешиваются – усредняются. Полученное таким образом размытие обладает рядом замечательных свойств – размывается только движущийся объект, причем размытие тем сильнее, чем быстрее он движется.
Размывается не только сам объект, но и его тени, подсветки, прозрачность и т.д. Сохраняется видимость объектов, находящихся за движущимся объектом. Единственное обязательное условие – возможность вычислить координаты нового положения объекта в любой момент времени. Совершенно замечательно то, что с точки зрения стоимости вычислений motion blur оказывается не дороже обычных вычислений DRT, поскольку каждый из промежуточных кадров может быть связан не со всеми сэмплирующими лучами, а только с одним из них. То есть, каждый из сэмплирующих лучей в корне лучевого дерева связывается с определенным значением промежуточного времени, и расчет соответствующей ветви лучей запускается только в это время. Каждая промежуточная картинка будет гораздо ниже по качеству, но в результате усреднения по времени мы получим вполне пристойный результат. В общем, на все это можно посмотреть и так – ветвям лучевого дерева присваивается определенное время, когда они рассчитываются. Каждому моменту времени соответствует новое положение объекта, поэтому каждая ветвь будет давать разные картинки, отличающиеся положением движущегося объекта, в конце все усредняется.
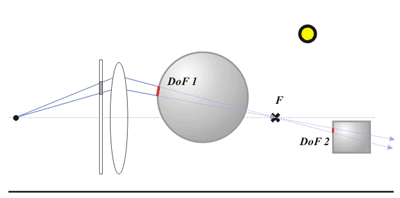
Depth of field, или размытие изображений объектов в соответствии с их положением относительно фокуса оптической линзы, получается самым естественным образом. Перед видовой плоскостью пикселов изображения помещается воображаемая линза с некоторыми оптическими характеристиками. Первичные лучи каждого пиксела, начальные направления которых определяются положением наблюдателя и пиксела на видовом окне, попадают на линзу и там искривляются так, чтобы после выхода из линзы пройти через ее фокусную точку.
Таким образом, после выхода из линзы первичные лучи пиксела сходятся в одной точке – точке фокуса и образуют конус лучей, вершина которого лежит в фокусе линзы. Диаметр сечения конуса будет тем больше, чем больше расстояние от сечения до вершины конуса (фокусной точки). Поэтому, если лучи пересекаются с поверхностью вне фокуса (объект находится ближе или дальше фокуса линзы), поверхность объекта будет размываться пропорционально величине расстояния от точек пересечения до точки фокуса, поскольку они будут распределены по сечению большего диаметра, то есть расстояние между ними будет больше, и усреднение значений приведет к большему размытию.

Яблоки .Depth of field (dof),3ds max 6, mray 3.2

Звонок (dof), автор – Andreas Bystrom

Пружина (dof)
Итак, стандартные возможности distributed (stochastic) ray tracing:
сэмплирование пиксела подавляет aliasing;
сэмплирование линз камеры создает depth of field;
сэмплирование во времени приводит к motion blur;
сэмплирование отражений (reflection) размывает отражения;
сэмплирование преломлений (transmission) размывает прозрачность;
сэмплирование источников света дает мягкие тени с размытыми краями (penumbras);
сэмплирование длин волн света (wavelength) позволяет рассчитывать дисперсию.
Глава 5. Оптимизация расчетов
Учитывая огромный объем работы, выполняемой лучевым трейсером, одним из важнейших сторон его реализации является оптимизация вычислений.
Известно, что 95% времени расчетов тратится на обнаружение пересечений. Если решать задачу "в лоб", придется для каждого луча проверять пересечение со всеми (!) полигонами в трехмерной сцене. Поэтому, главное направление поисков оптимизации – выработка правил исключения геометрии из расчетов без реальной проверки пересечений (вычислять меньше пересечений), затем – разработка алгоритмов быстрого вычисления пересечений, и наконец – обобщение лучей (beams, cones, pencils).
Bounding Volumes
Один из методов уменьшения количества тестов пересечения. Полигональный объект или группа объектов окружаются одной общей замкнутой поверхностью простого вида, например сферой или кубом. Для простых поверхностей (сфера, куб и другие) тесты пересечений выполняются достаточно быстро. Главное требование – чтобы объекты как можно полнее заполняли внутренний объем такой поверхности, с наименьшим количеством пустот. Тогда для всей такой группы можно выполнить только один тест пересечения луча с окружающей поверхностью. Если пересечения нет, вся группа объектов исключается из дальнейших тестов для данного луча. Очевидно, можно использовать вложенные bounding volumes, создавая иерархию простых поверхностей (hierarchical bounding volumes, иногда их еще называют directed acyclic graph – DAG), содержащих только по одному объекту или даже отдельные части трехмерного объекта. Если луч пересекается с поверхностью, окружающей всю группу объектов, то выполняются дополнительные тесты вложенных поверхностей в соответствии со структурой DAG. Разработка эффективной структуры вложенных поверхностей невозможна без вмешательства человека.
Kay и Kajiya разработали следующие рекомендации для построения эффективных иерархических диаграмм (деревьев):
любой вложенный объем должен содержать близко расположенные объекты; чем больше степень вложенности окружающего объема, тем ближе должны быть объекты в него входящие;
окружающий объем должен быть минимален по размеру;
сумма всех окружающих объемов также должна быть минимальной;
конструкция дерева иерархии окружающих объемов должна основываться на тщательной разработке узлов вблизи корня (т. е. самого верхнего объема, включающего все остальные).
Spatial Subdivision
Spatial Subdivision, или пространственное разбиение, использует несколько иной подход. Этот метод разбивает все трехмерное пространство на непересекающиеся регионы по высоте, ширине и глубине. Преимущества – позволяет учесть направление луча (сортировка регионов по высоте-ширине) и тот факт, что пересечение ищется только с самой близкой поверхностью (сортировка регионов по глубине).
Пространственное разбиение может быть однородным, то есть разбиваться на одинаковые области, и неоднородным, когда плотность разбиения зависит от количества объектов в данной области пространства. Пространственное разбиение позволяет создавать различные иерархические структуры данных, которые используются лучевыми трейсерами в тестах пересечений.
Примером неоднородного разбиения являются так называемые octree-структуры, идею которых предложил Glassner. Пространство разбивается на восемь кубических регионов рекурсивно, пока не будет выполнено некоторое простое условие, регионы (sub-octree) индексируются. Самый первый octree называют "world" (мир), самый маленький с наибольшей глубиной вложенности – voxel (воксель).
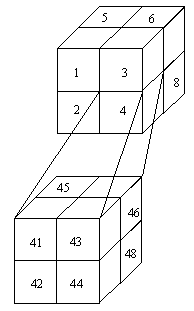
Пример разбиения пространства на octree
и индексации вложенных sub- octree
Каждый воксель помечается как пустой, заполненный или смешанный (частично заполненный). Octree-структура содержит имя каждого вокселя (индекс), флаг разбиения и список объектов, пересекающих данный воксель. Этот метод показывает хорошие результаты для сцен с большим количеством объектов, плотность распределения которых в пространстве меняется.
Еще один метод разбиения пространства носит название binary space partitioning (BSP) – двоичное разбиение пространства. Это неоднородное разбиение пространства, при котором каждый регион содержит в себе два вложенных, разбиение производится плоскостями, параллельными осям x, y, z. Например, сначала все пространство разбивается на две части одной плоскостью (z), затем каждая новая часть независимо разбивается еще на две части другой плоскостью (y) и т.д. В результате получается двоичное дерево, одним из важных свойств которого является возможность корректного определения видимости любой поверхности из любой точки наблюдения.
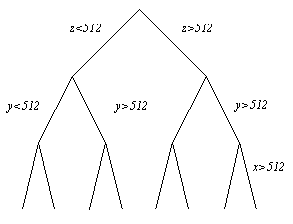
Двоичное дерево разбиения пространства
методом BSP
Light buffer
Light buffer (иногда еще используется название shadow buffer) используется для ускорения расчета теней. Поскольку такие расчеты являются определением закрывающего свет объекта между точкой поверхности и источником освещения, они являются тестами пересечения вторичных теневых лучей со всеми объектами сцены. Идея состоит в том, чтобы окружить каждый источник кубом, разбить каждую из шести граней куба на ячейки и затем спроектировать на них окружающие источник объекты. Таким образом, каждая ячейка грани будет соответствовать некоторому направлению на источник и содержать информацию о перекрывающих ее объектах сцены в упорядоченном по глубине от источника списке. Вместо тестов пересечений можно просто просматривать списки, хранящиеся в light buffer.
Когеренция лучей
Этот метод ускорения использует для расчетов текущего луча расчеты, выполненные для предыдущего луча и его ветви. Вычисленная ветвь используется для предсказания пересечений следующей ближайшей ветви, для чего вокруг каждого луча строится так называемая "зона безопасности", в пределах которой нет новых объектов, кроме того, с которым пересекается данный луч. Если новый луч не выходит за пределы безопасности предыдущего луча и пресекает тот же объект, тогда новый луч не пересечется с другим объектом. В противном случае, вероятно пересечение с объектом, хранящимся в "кэше" (ближайший к данному другой объект).
Когеренция лучей также интенсивно используется в алгоритмах лучевых трейсеров реального времени.
Обобщенные лучи
Используемые обычно при рейтресинге лучи обладают длиной, но не имеют толщины. Предпринимаются попытки использования лучей, имеющих определенную "толщину" – конусообразные (cone), beam и pencil. Обобщение лучей приводит к таким преимуществам, как более эффективное использование метода когеренции лучей, более эффективный антиалиасинг и дополнительные оптические эффекты.
Заключение
DRT очень качественный и очень "дорогой" метод расчетов, способный "положить" любой современный компьютер. Поэтому, в настоящее время большинство рендеров общего назначения используют сочетание: скан-лайн плюс рейтресинг только там, где это необходимо. Такой подход позволяет получать высокое качество за приемлемое время.
Метод Монте-Карло позволяет эффективно решать и гораздо более сложные уравнения рендеринга, чем те, которые используются в DRT, и рассчитывать тем самым более сложные взаимодействия света и поверхностей объектов. Прежде всего имеется в виду, конечно же, учет вторичного диффузного рассеяния света объектами и другие, в частности – caustic. Но об этом мы поговорим в следующей части, посвященной radiosity и методу фотонных карт.