Ваш город: Москва
Как компьютер рассчитывает изображения. Технологии программного рендеринга. Часть 2

Andreas Bystrom. Голливудский атлетический клуб
В первой части рассмотрена локальная модель освещения, скан-лайн рендеринг, классический рекурсивный ray tracing, distribution (stochastic) ray tracing, antialiasing.
Глава 6. Radiosity
Как мы выяснили в первой части, и скан-лайн рендер, и рейтресинг рассчитывают диффузную освещенность трехмерных поверхностей только от прямых источников света в соответствии с законом Ламберта. Учитывая, что диффузная освещенность несет основную визуальную информацию о геометрии и цвете объектов, совершенно очевидно, что только закона Ламберта для достижения фотореалистичных результатов расчета освещенности недостаточно. В частности, при расчете диффузного освещения данной поверхности необходимо учесть не только ее освещение прямыми источниками света, но и так называемое вторичное (или отраженное) диффузное освещение – диффузное рассеяние света окружающими объектами.
Метод расчетов, позволяющих учесть вторичное диффузное освещение, получил название radiosity, или метод излучательности. Radiosity – яркий пример красоты используемых идей и эффектности получаемых результатов, позволяющих компьютерным изображениям вплотную приблизиться к грани совершенства.
Для получения уравнений radiosity делается несколько основных допущений. Первое – поверхности всех объектов трехмерной сцены разбиваются на плоские небольшие участки – патчи (patch). В некотором смысле они напоминают полигоны, с помощью которых описываются поверхности, хотя на самом деле таковыми не являются. То есть, они могут быть больше или меньше размера реальных полигонов и по сути являются модельным инструментом radiosity, а не средством точного описания поверхности. Размер каждого патча должен быть настолько мал, что плотность распределения интенсивности световой энергии в его пределах можно считать постоянной величиной (константой). И наконец, считают, что диффузное рассеяние света не зависит от угла, то есть свет рассеивается равномерно по всем направлениям. Такой подход для получения и решения уравнений освещенности radiosity получил название finite element method – метод ограниченных элементов.
Основные идеи radiosity заимствованы из физики теплового переноса, оперирующей такими понятиями, как поток энергии и плотность потока энергии. Потоком энергии (вообще – тепловой, но в нашем случае – световой) называют количество энергии, проходящей через некоторую площадь в единицу времени. Плотностью потока энергии называют поток энергии, проходящий через единицу площади. Другими словами, плотность потока энергии – это количество энергии переносимой через единицу площади в единицу времени. В физике теплопереноса считается, что поток энергии некоторой поверхности состоит из двух частей – собственной энергии, излучаемой самой поверхностью, и энергии, приносимой в данную поверхность извне – от других поверхностей. Опять же, учитывая нашу специфику, можно сказать, что под собственной энергией поверхности мы можем понимать диффузное рассеяние света от прямого источника (это также может быть еще и самосветимость объекта, поэтому дальше я буду использовать термин "собственная эмиссия" патча, поскольку он является наиболее общим), а под приносимой энергией – освещение, отраженное диффузно всеми окружающими объектами. Сама величина radiosity определяется как плотность потока энергии, испускаемой патчем (покидающей патч). Таким образом, radiosity – это поток энергии, исходящей от единицы площади поверхности в единицу времени.
Как рассчитать энергию от прямого освещения известно – это все тот же закон Ламберта. Чтобы учесть вторичное диффузное отражение окружения, воспользуемся модельными допущениями, о которых я говорил выше. А именно, плотность потока энергии, приходящей в данный патч, является суммой потоков от всех остальных патчей. Поток энергии каждого из окружающих патчей вычисляется как произведение площади такого патча на плотность испускаемого им потока энергии (т.е. radiosity этого патча), поскольку патч настолько мал, что плотность потока в его пределах можно считать постоянной величиной. И наконец, необходимо учесть взаимную ориентацию и расстояние патчей. Для этого вводится так называемый форм-фактор. Форм-фактор просто определяет, какая часть всего потока излучаемой энергии (radiosity) данного патча достигает другого патча (как он вычисляется – расскажу чуть позже). Вследствие всего этого, основные уравнения расчета radiosity имеют следующий вид:

Основные уравнения radiosity. Еще используется название "матричные уравнения радиосити".
И получили название matrix radiosity, то есть – матричная радиосити.
С математической точки зрения мы здесь имеем n уравнений для нахождения n неизвестных, то есть все значения радиосити можно найти совершенно точно, хотя бы теоретически. Практически дело осложняется тем, что в реальной сцене патчей должно быть много. Если например, считать, что размер патча равен размеру полигона, то в сцене из 1 миллиона полигонов (что по нынешним временам вовсе не редкость) мы будем иметь миллион патчей, то есть нужно будет решить систему из миллиона уравнений! Кроме того, для каждого патча должно быть вычислено n форм-факторов, определяющих вклады от всех остальных патчей сцены, а для всех n патчей – nxn форм-факторов. Для сцены из миллиона патчей эта цифра составит 10^12. Если использовать по 1 байту на фактор, для хранения всех значений потребуется около 1000 гигабайт. Это означает, что прямое математическое решение уравнений методом исключения Гаусса неприемлемо как с точки зрения времени вычислений, так и количества памяти для хранения переменных (радиосити патчей и форм-факторов). Поэтому, хотя основные уравнения радиосити имеют универсальное значение, для их решения используются различные подходы, что и привело к появлению разновидностей алгоритмов расчета радиосити.
Одним из самых первых алгоритмов стал метод итераций Гаусса-Зейделя (Gauss-Seidel iteration). Его суть в пошаговом вычислении радиосити патчей с последующей корректировкой промежуточных значений (называемых оценочными значениями). На самом первом шаге считается, что вторичное отражение отсутствует, тогда радиосити всех патчей равны их собственной эмисси. На следующем шаге вычисленное промежуточное значение радиосити подставляется в уравнение, и находится новое промежуточное значение, которое будет отличаться по значению в большую сторону. Поскольку для реалистичных поверхностей коэффициент диффузного отражения меньше единицы, и любой из форм-факторов также всегда меньше единицы (описывает часть от целого значения), добавка к промежуточному значению радиосити с каждым шагом вычислений будет все меньше и меньше. Наконец, и это может быть совершенно точно доказано математически, на определенном шаге итерации новое промежуточное значение не будет отличаться от предыдущего вычисленного значения в пределах заданной точности. Тогда считается, что искомое значение радиосити найдено. Хотя этот метод решает часть проблем вычисления значений радиосити, он все еще недостаточно быстр и требует такого количества памяти для хранения переменных, что его использование для решения практических задач почти невозможно.
Второй, и наиболее распространенный, метод решения уравнений радиосити носит название метода прогрессивного уточнения оценок (progressive refinement method).
Если посмотреть еще раз на основные уравнения radiosity, можно увидеть, что они рассчитывают радиосити данного патча как сумму вкладов радиосити от окружающих патчей, при этом всякий раз используются все форм-факторы в количестве nxn, где n – количество всех патчей. Это равносильно тому, что мы собираем в данном патче свет, диффузно отраженный от окружающих поверхностей. Основные уравнения radiosity путем математических преобразований можно привести к такому виду, что они будут описывать вклад данного патча в радиосити всех остальных патчей, то есть наоборот – не собираем свет, а излучаем свет из данного патча в направлении окружающих поверхностей:

Формула вычисления вклада от одного патча (пусть, для определенности, это будет самый первый) в радиосити других патчей.
Такой подход имеет то преимущество, что при вычислении вкладов требуется только n форм-факторы того патча, вклады которого вычисляются.
В практических вычислениях используется следующий алгоритм:
1. На первом шаге итерации считается, что отраженного света пока нет, поэтому радиосити всех патчей определяются освещенностью прямыми источниками света в соответствии с законом Ламберта + собственное излучение, если патч принадлежит самосветящейся поверхности.
Вычислений форм-факторов тоже пока не требуется. По найденным значениям радиосити производится упорядочивание патчей в порядке убывания. Это делается для того, чтобы в последующих итерациях вычисления начинались с патчей, обеспечивающих самые существенные вклады. Поскольку речь идет об отраженном свете, это же означает, что такие патчи будут и наиболее сильно освещенными.
2. Выбирается первый патч последовательности (наиболее освещенный), и в соответствии с формулой рисунка выше вычисляются вклады первого патча в радиосити всех остальных патчей. Вычисленные вклады суммируются с радиосити соответствующих патчей и сохраняются с накоплением в так называемой переменной неизлученной радиосити (unshoot radiosity) соответствующего патча для следующей итерации (то есть, вклад первого патча в радиосити второго патча прибавляется к радиосити второго патча и суммируется со значением переменной неизлученной радиосити второго патча). Unshot radiosity первого патча обнуляется после вычисления всех вкладов первого патча – вся "неизлученная" освещенность теперь "излучена". Таким образом, каждый патч характеризуется текущим значением радиосити и переменной неизлученной радиосити, представляющей собой сумму вкладов от других патчей, вычисленных в текущей итерации.
При вычислении вкладов от второго патча (и последующих) используется накопленная к этому моменту неизлученная радиосити как сумма вкладов от уже обсчитанных патчей (в данном случае – предыдущего, первого патча). После вычислений всех вкладов переменная unshot radiosity второго патча тоже обнуляется, но ее значение будет меняться в процессе итерации в результате последующих вычислений других патчей. Так, значение неизлученной радиосити первого патча, которую мы обнулили раньше, теперь будет равна величине вклада второго патча в радиосити первого патча. Итерация заканчивается, когда будут вычислены вклады всех патчей.
Использование unshot radiosity имеет простую интерпретацию – это свет, излученный патчем в направлении окружающих поверхностей и отраженный назад. С каждой итерацией мы снова и снова излучаем этот свет, интенсивность его при этом все время уменьшается, что и обеспечивает сходимость, то есть – конечное число итераций при вычислении полного значения радиосити.
3. Итерации выполняются до тех пор, пока значение максимального вклада какого-либо патча не станет меньше некоторой заданной величины.
Пример:
Пусть в нашей сцене имеется всего три патча и один источник света E1. Присваиваем значениям радиосити B(i) и неизлученной энергии U(i) каждого патча величину их диффузной освещенности от источника света E1(i). Упорядочиваем патчи по величине B, пусть самое большое значение будет у 1-го, затем у 2-го и у 3-го. На второй итерации берем первый патч и используя его значение U(1) находим вклады во второй и третий патчи. Вклады суммируем со значением радиосити B(2) и B(3), а также приплюсовываем их к неизлученной энергии U(2) и U(3). Затем обнуляем значение U(1) – вклады от нее уже рассчитаны, то есть энергия "излучена". Переходим ко второму патчу, используя его значение неизлученной энергии U(2) = E(2) + вклад от первого патча, рассчитываем вклады в первый и третий патчи, обновляем значения радиосити и неизлученной энергии для 1 и 3 патчей, U(2) обнуляем. Переходим к третьему патчу, его значение U(3) = E(3) + вклад от первого патча + вклад от второго патча используется для рассчета вкладов в первый и второй патч. После вычисления вкладов U(3) обнуляется. Первая итерация завершена, переходим к следующей и т.д.
Выигрыш в скорости расчетов и экономия необходимой для вычислений памяти в progressive refinement method оказались настолько велики, что этот метод впервые позволил реализовать расчет radiosity в практических приложениях и даже успешно применяется в приложениях реального времени.
Третий метод решения уравнений носит название wavelet radiosity. Wavelet метод использует динамическое представление поверхностей патчами в зависимости от расстояния поверхностей друг от друга. Например, если поверхность А расположена далеко от поверхности Б, то для расчета вклада радиосити от поверхности А используется грубое представление большими патчами поверхности А. Если рассчитывается радиосити поверхности С, расположенной близко к А, то в этом случае А описывается точно, большим количеством патчей.
Matrix radiosity, wavelet radiosity и progressive refinement являются основными разработанными методами вычислений. В практических приложениях в основном используется усовершенствованный progressive refinement method with substructuring (адаптивно разбивает патчи на более мелкие по площади в областях с тоновым градиентом – например, на границах теней), wavelet radiosity – очень редко.

Progressive refinement radiosity с адаптивным разбиением патчей в областях тоновых градиентов.
Сравнения этих методов, предпринимавшиеся неоднократно (см., например "An Empirical Comparison of Progressive and Wavelet Radiosity"), показывают, что progressive refinement дает лучшие результаты в простых сценах, wavelet radiosity – в больших сложных сценах с множеством объектов. Однако, wavelet radiosity использует гораздо большее количество памяти в вычислениях.
В конце прошлого тысячелетия :), а именно – в конце 90-х годов, был разработан еще один способ решения основных уравнений радиосити, получивший название Stochastic Relaxation Radiosity, или SRR. Именно этот алгоритм расчетов применяется в 3ds max, начиная с шестой версии, он основывается на применении метода Монте-Карло (М-К) как для решения матричных уравнений радиосити, так и уравнений progressive refinement method. В данном случае метод М-К используется для оценки величины суммы вкладов радиосити всех патчей в данный (или вкладов данного патча во все остальные патчи) по величине вкладов части из них. Другими словами, этот метод позволяет вычислять не все вклады, а только часть из них, выбранных по некоторому случайному закону. Кроме того он же позволяет при вычислениях вкладов избежать вычислений форм-факторов. Общий алгоритм таков:
Берем первый патч и на его поверхности некоторым случайным образом выбираем N точек. Из каждой точки под некоторым случайным углом испускается луч. Луч трассируется до пересечения с ближайшим патчем. Вероятность того, что луч пересечет именно этот патч, а не другой, определяется величиной форм-фактора двух соответствующих патчей. Именно это обстоятельство позволяет исключить вычисление форм-фактора из вычислений вкладов. Вклад i-го патча, с которым пересекся луч (или вклад в i-й патч) вычисляется по формуле:
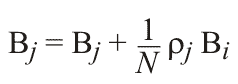
После расчета вкладов от N случайных патчей, переходим к следующему патчу. После перебора всех патчей данная итерация закончена, переходим к следующей, пока величина вкладов не станет меньше заданной величины.
Из приведенного алгоритма хорошо видно, что для каждого выбранного патча расчет вкладов в него от всех остальных патчей заменяется на расчет N вкладов от случайно выбранных патчей, где N – число сэмплирующих поверхность патча лучей. В теории Stochastic Relaxation Radiosity получены математические формулы, определяющие количество сэмплирующих лучей N в зависимости от требуемой точности вычисления значений радиосити. Значение N индивидуально для каждого патча сцены и вычисляется для каждого патча по отдельности, но один раз для всех итераций. Кроме того, при вычислении N требуется рассчитывать значения форм-факторов данного патча со всеми остальными, так что совсем без форм-факторов обойтись все же не удастся.
Stochastic Relaxation Radiosity обеспечивает гораздо более быстрый расчет радиосити и требует меньше памяти для вычислений, чем все другие рассмотренные методы. Как я уже говорил, практическую реализацию этого метода можно увидеть на примере расчетов радиосити в 3ds max 6. Есть одно обстоятельство, которое необходимо учитывать при использовании SRR – случайность природы расчетов. Это значит, что вполне вероятны ситуации, когда некоторые мелкие детали в сцене могут "выпасть" из расчетов, если лучи в них не "попали". Для исправления такого положения алгоритм расчета радиосити предусматривает механизм дополнительного сбора (regathering) излучения за счет испускания дополнительных лучей.
Любой из вышеописанных методов рассчитывает radiosity для всего патча. Если предположить, например, что размер патча равен размеру полигона, мы получаем, что значение радиосити постоянно в пределах полигона, аналогично модели затенения Facet. Для сглаживания значений радиосити между полигонами используется модель затенения Гуро – вычисляется значение radiosity для каждой вершины как усредненное значение радиосити примыкающих к ней полигонов, цвет точки внутри полигона интерполируется по вершинам способом, который был рассмотрен в первой части. Интерполяцию значений радиосити между полигонами по Гуро и метод разделения на патчи можно считать одними из самых существенных недостатков радиосити, поскольку для "гладкого" представления радиосити-освещенности может потребоваться большое количество патчей. Если сцена сложная и большая, радиосити вообще может не поддаваться вычислению из-за требований огромного количества памяти и времени.
Вычисление форм-фактора
Форм-фактор i-го патча определяет, какая часть радиосити j-го патча достигнет i-го патча. Форм-фактор должен учитывать площади обоих патчей, их взаимную ориентацию и расстояние между ними.
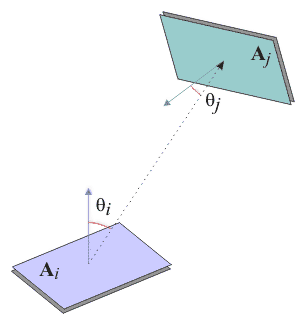
Схема вычисления форм-фактора для пары патчей
В самом общем виде формула вычисления форм-фактора выглядит следующим образом:
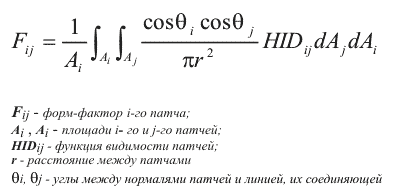
Формула расчета форм-фактора для пары патчей.
Эта формула не учитывает влияния среды, в которой распространяется свет (дым, пыль, туман и т.д.). Аналитическое решение этого интеграла в общем случае невозможно, поэтому для его нахождения используются различные численные методы и упрощения.
В одном из способов расчета считается, что первый патч – точка. В эту точку помещается полусфера единичного радиуса, второй патч проектируется сначала на поверхность сферы, затем – на ее основание. Величина форм-фактора тогда будет равна отношению дважды спроектированной площади второго патча к площади основания полусферы.
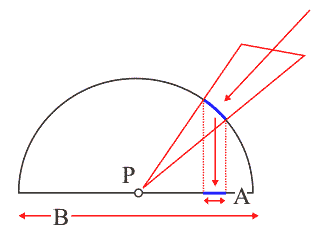
Расчет форм-фактора для пары патчей с использованием полусферы. Первый патч – точка, в которую помещается центр единичной полусферы. Второй патч проектируется сначала на поверхность сферы, затем – на ее основание. Форм фактор равен отношению спроектированной площади второго патча к площади основания полусферы.
Другой способ вычислений использует вместо полусферы полукуб, с гранями, разделенными на ячейки. Патч проектируется на полукуб, вычисляются соответствующие ячейки, форм-фактор патча равен сумме форм-факторов ячеек, на которые "упала тень" патча.
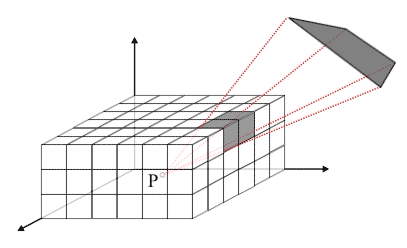
Расчет форм-фактора с помощью полукуба
Преимущества и недостатки radiosity
Расчет методом радиосити позволяет точно находить диффузную освещенность сцен, тени от объектов, перенос и смешивание отраженного цвета с одних поверхностей на другие (color bleeding). Интересно также то, что выполненный расчет освещенности не зависит от положения наблюдателя – в отличие от рейтресинга, в уравнениях радиосити никак не используется точка положения наблюдателя . То есть, если анимация в сцене обусловлена только перемещением камеры, можно использовать одно и то же найденное распределение освещенности до тех пор, пока не изменится взаимное положение объектов сцены или освещение.
К недостаткам радиосити следует отнести невозможность расчета отражений и преломлений вблизи идеальных (зеркальных) углов, трудности в расчете больших открытых сцен, что ограничивает применение radiosity расчетами освещенности закрытых помещений. Достаточно сложно в рамках этой модели использовать и методы antialiasing.
Кажется вполне логичным соединить два метода расчета освещенности – radiosity и ray tracing. Такое объединение может быть выполнено математически совершенно строгим образом – введением когерентного излучения в исходную модель radiosity. Однако, получающиеся интегралы освещенности сложны даже для численных методов, а соответствующие алгоритмы очень трудоемки. Поэтому часто используют другой способ объединения. На первом этапе рассчитывают диффузную освещенность методом radiosity и сохраняют ее значения в вершинах геометрии для последующего интерполирования в точках пересечения с лучами ray tracing. На втором этапе запускается расчет ray tracing, лучи которого "поднимают" вторичную диффузную освещенность из точек пересечения с поверхностью. Однако, эта комбинация не сработает на чисто зеркальных поверхностях, поскольку radiosity рассматривает только диффузное отражение и неприменима для прозрачных поверхностей, поскольку радиосити вообще таковые не рассматривает. Эта трудность может быть преодолена расчетом новых, расширенных форм-факторов патчей. Для этого используется все тот же метод трассировки лучей, испущенных из точки поверхности через каждую ячейку полукуба назад в трехмерную сцену. Для таких лучей находятся пересечения с другими поверхностями методом рекурсивного рейтресинга.
Таким образом, расширенный форм-фактор позволяет определять и диффузное отражение, и когерентное (под одним углом) отражение, и преломление для каждого патча, а в целом, расчет radiosity плюс ray tracing позволяет рендерам использовать все преимущества обоих методов. Расчет расширенных форм-факторов довольно просто осуществляется в методе SRR (Stochastic Relaxation Radiosity), поскольку он основывается на испускании лучей каждым патчем. Многие программы трехмерного моделирования обладают такими синтетическими двухпроходными рендерами. В качестве примера можно привести LightWave и 3ds max.
Только прямое освещение. Скан-лайн рендер 3ds max 6.
Только радиосити, без прямого освещения от источников света. Хорошо заметен шум и полигонная структура сферы – результат использования модели Гуро для сглаживания значений радиосити для разных патчей (полигонов). Радиосити рендер 3ds max 6.
Увеличение точности решения радиосити и количества патчей не устранили шум на сфере. На кубе и конусе шум отсутствует. Радиосити рендер 3ds max 6.
Совместная работа скан-лайн рендера, рейтресера (тени) и радиосити 3ds max 6. Шум не наблюдается, поскольку значения радиосити используются как добавка к расчету прямого освещения, использующего модель Фонга. 3ds max 6.
Сфере назначен прозрачный материал. Пример совместной работы радиосити и рейтресинга 3ds max 6. Хорошо заметен color bleeding – голубоватый оттенок на окружающих сферу объектах.
Сфере назначен отражающий материал и прозрачный материал – конусу. Скан-лайн рендер, рейтресинг, радиосити 3ds max 6.
Глава 7. Photon Mapping
Поскольку и стохастический рейтресинг, и радиосити очень неплохо справляются с решением своего круга задач, неоднократно предпринимались попытки расширения одного из методов, чтобы исключить необходимость использования другого. Однако, такой подход является неестественным, настоящее решение лежит на пути объединения обоих методов. Один из таких способов объединения был предложен Henrik Wann Jensen (Хенрик Ванн Йенсен) и получил название "расчет глобальной освещенности методом фотонных карт" (Global Illumination using Photon Maps). На мой взгляд, название "метод фотонных карт" несколько запутывает суть дела, правильнее было бы называть этот способ расчетов "гибридным двухпроходным рейтресером", поскольку это точнее соответствует его сущности. Однако, обо всем по порядку.
Итак, метод фотонных карт состоит в расчете освещенности точек поверхности трехмерных объектов в два прохода. На первом проходе выполняется прямая трассировка испущенных источником света полных траекторий лучей от момента их испускания источником через все возможные многократные взаимодействия с поверхностями и до момента поглощения света какой-либо из них. Результат отслеживания траекторий сохраняется в базе данных, получившей название "фотонная карта". На втором проходе выполняется расчет освещенности пикселей изображения методом обратного стохастического рейтресинга с использованием данных фотонных карт. Рассмотрим каждый из этапов более подробно.
Первый проход, прямая трассировка лучей
Источник света, пространственный или объемный, разбивается на участки, каждый участок испускает пучок лучей вглубь трехмерной сцены. Количество лучей в таком пучке зависит от функции плотности распределения интенсивности источника света, сложности сцены, а также – от требуемой точности вычисления освещенности. Каждый луч является траекторией испускаемой порции энергии освещения, а сама излучаемая энергия называется фотоном. В данном случае "фотон" – это порция энергии излучения, термин компьютерной графики, не имеющий ничего общего с реальным фотоном света. Траектория каждого фотона прослеживается до ближайшего пересечения с поверхностью. Как только фотон достигает поверхности, принимается решение о том, как он будет взаимодействовать с ней. Возможны следующие варианты. Фотон может быть поглощен, диффузно рассеян, отражен вблизи зеркального угла (specular или glossy reflection), преломлен прозрачной поверхностью диффузно или вблизи идеального угла преломления. Какое именно из этих событий произойдет с данным конкретным фотоном, решается совершенно случайным образом при помощи метода "Русской рулетки".
А именно, при достижении очередной поверхности фотону сопоставляется число k со значением от 0 до 1, полученное при помощи генератора случайных чисел. Это число сначала сравнивается с коэффициентом диффузного отражения/преломления поверхности, взаимодействие с которой рассматривается. Если оно меньше, фотон диффузно рассеивается под некоторым углом, а в базе данных для этой поверхности (фотонной карте поверхности) сохраняется запись о рассеянном фотоне: координаты его пересечения с поверхностью, значение энергии и направление падения на поверхность. (Примечание: запись о фотоне сохраняется в любом случае, если поверхность имеет диффузные свойства). Такие записи делаются для взаимодействий фотонов только с диффузными поверхностями и кроме самой первой. Исключение первой поверхности вызвано тем, что освещенность от прямого источника света (а это и есть диффузное рассеяние фотона первой поверхностью) вычисляется рейтресингом на втором проходе, и учет этого рассеяния еще и в фотонной карте приведет к дублированию освещенности точки прямым источником света. Если k больше коэффициента диффузного рассеяния поверхности, и для поверхности определены свойства зеркального отражения, и задан коэффициент отражения (или преломления, это подразумевается везде далее в тексте), k сравнивается с сумой коэффициентов диффузного преломления и отражения. Если k меньше этой суммы, фотон отражается (specular или glossy) на некоторый угол вблизи угла идеального отражения. Запись в фотонной карте не делается, если поверхность обладает только свойствами отражения и не имеет диффузных свойств, поскольку результат зеркальных отражений зависит от положения наблюдателя. Наконец, если k больше суммы коэффициентов диффузного и зеркального отражений (или преломления), фотон поглощается поверхностью, и его траектория обрывается. Во всех случаях отражения фотона его энергия уменьшается на некоторую величину. Таким образом отслеживаются все первоначально испущенные источником света лучи либо до момента их полного поглощения, либо до заданного количества взаимодействий с поверхностями сцены, называемого глубиной трассировки.
В наиболее общем случае, если для поверхности задана BRDF (или BTDF для прозрачной поверхности), угол, на который рассеивается фотон после взаимодействия, определяется этой функцией. Напомню, что BRDF – Bidirectional Reflectance (Transmitted) Distribution Function, определяется как функция вероятности отражения поверхностью под углом j луча, падающего под углом i. Таким образом, BRDF поверхности определяет, под каким углом будет отражен после взаимодействия фотон, и все что ей для этого потребуется – знать направление падающего фотона.
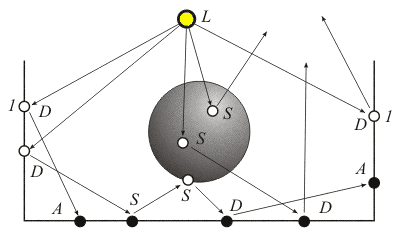
Первый проход, прямая трассировка лучей от источника света. Пол и стены комнаты являются диффузным и отражающим материалом (свойства поверхности описываются BRDF), сфера – зеркально отражающим материалом. A – поглощение фотона, D – диффузное рассеяние, S – зеркальное отражение, 1 – первое взаимодействие фотона с поверхностью. Черная точка означает запись в фотонной карте, белая точка – отсутствие записи. Пол и стены комнаты будут иметь фотонные карты, сфера – нет.
После поглощения всех фотонов первый проход считается законченным. Его результатом является создание фотонных карт для каждой из поверхностей в сцене, имеющей хоть какие-то диффузные свойства. Фотонная карта каждой поверхности хранит данные только о фотонах, рассеянных этой поверхностью и не содержит данных о фотонах прямого освещения. Насколько мне известно, сейчас для представления информации об одном фотоне используется 20 байт. Кроме того, не все испущенные фотоны будут сохранены в картах – часть просто уйдет в окружающее пространство или же поглотится при самом первом пересечении с поверхностью. Часть "пропавших" фотонов может быть достаточно велика.
Как я уже говорил, "фотонная карта" является базой данных о провзаимодействовавших с поверхностью фотонах. Основные цели такой базы данных – хранение записей о фотонах для многократного использования при вычислениях на втором проходе и быстрый поиск N записей о фотонах вблизи заданного. Реализована такая база данных в виде сбалансированной иерархической kd-tree структуры. При этом, сначала выполняются записи обо всех диффузных рассеяниях в том порядке, как они происходят при трассировке, а после поглощения всех фотонов выполняется упорядочивание записей в базах данных. Упорядочивание происходит следующим образом. Для данной поверхности берутся фотоны с максимальным и минимальным значением координат, и вычисляется их разница. Полученное значение делится пополам и прибавляется к координатам с минимальным значением. Затем ищется фотон, чьи координаты ближе всего соответствуют этим значениям, и через него проводится прямая линия параллельно одной из координатных осей, разбивающая всю группу фотонов на две части. Далее процесс повторяется, пока в группах не останется заданное количество фотонов (как правило – один).
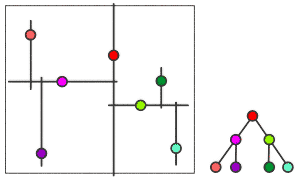
Пространственное положение фотонов и их упорядочивание в kd-структуру.
Таким образом формируется древовидная структура, в каждом узле которой содержится фотон c указателем на два ближайших узла. Интерактивную демонстрацию процесса создания такой структуры можно посмотреть, например, вот по этому адресу (требуется поддержка Java 1.1).
Фотонные карты являются обобщением метода illumination-карт, предложенного Arvo. Это растровые карты, используемые для хранения информации о пересечениях лучей и поверхностей. Однако такие карты не могут быть использованы для параметрических поверхностей. Таким образом, фотонные карты являются обобщением карт Arvo на случай параметрических поверхностей. Детали об illumination map можно посмотреть вот в этой работе.
Теоретически, одной только прямой трассировки лучей от источника света достаточно для физически корректного вычисления всего спектра оптических явлений неволновой природы. И это не только отражения, преломления, тени, радиосити, но и caustic, subsurface scattering, объемные эффекты… Достижимо это при двух существенных условиях – количество лучей должно быть очень большим (в идеале – бесконечным), а глубина трассировки не ограничена. Тогда фотонные карты можно визуализировать напрямую, почти без дополнительных расчетов. Но дело в том, что время расчетов в этом случае становится неприемлемо большим (тоже стремится к бесконечности). Поэтому, в практических расчетах количество лучей ограничивается величиной в пределах от нескольких десятков тысяч до нескольких миллионов (от нескольких сотен до нескольких тысяч на один пиксел). Получаемые в этом случае фотонные карты непригодны для прямой визуализации, но являются прекрасным вспомогательным средством расчетов освещенности методом обратного рейтресинга. Возможность выбора количества лучей прямой трассировки делают метод фотонных карт гибким инструментом, позволяя использовать его как для точных расчетов освещенности архитектурных визуализаций, так и в индустрии развлечений, где требуется всего лишь правдоподобие освещенности, зато время расчетов очень критично.
В настоящее время разработано несколько расширений фотонных карт.
Одно из таких расширений позволяет рассчитывать и сохранять в фотонных картах вместе с обычными диффузными фотонами и так называемые теневые фотоны, уменьшающие количество лучей при вычислениях прямой освещенности методом обратного рейтресинга (теневых лучей) более чем на 90%. Расчет теневых фотонов выполняется следующим образом. При прямой трассировке луча находится первая поверхность пересечения. Далее луч просто продляется в том же первоначальном направлении, и фиксируются все его пересечения с другими поверхностями, при этом в фотонную карту каждой поверхности пересечения вносится запись о координатах теневого фотона, его направлении и принадлежности к тому или иному источнику света.
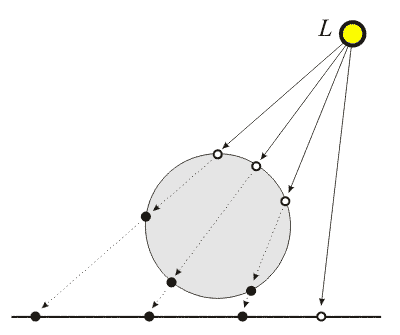
Построение теневых фотонов. Белые точки – нормальные фотоны, черные точки – теневые фотоны.
Когда на втором этапе рейтресинг вычисляет прямую освещенность точки, он сначала анализирует фотоны вблизи координат этой точки. Если все фотоны – обычные, и теневых нет, значит точка освещена. Если все фотоны теневые, значит точка в тени. Если присутствуют и те и другие фотоны, значит точка лежит на границе света и тени, и только тогда выполняется сэмплирование источника света лучами.
Второе и очень важное расширение фотонных карт – caustic фотонные карты, позволяющие вычислять области концентрации световых лучей на диффузных поверхностях после отражения или преломления зеркальными и прозрачными объектами. Пример таких явлений – сфокусированный линзой свет или световые блики от волн на дне и стенах бассейна. Вычисление таких явлений возможно только методом прямой трассировки лучей и требует большого их количества. Поэтому, специально для расчета caustic источники света целенаправленно испускают большое количество лучей с большой плотностью в направлении сильно отражающих или прозрачных объектов. После трассировки лучей до диффузной поверхности, где caustic-фотоны рассеиваются, для этой поверхности создается отдельная caustic фотонная карта, которая без дополнительной обработки, напрямую, визуализируется во втором проходе.
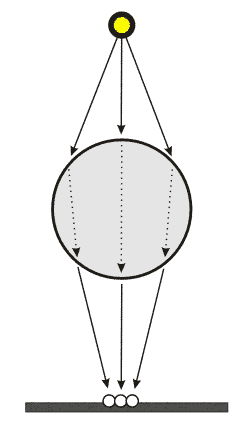
Явление caustic для случая прозрачной преломляющей сферы. Примером отражающего типа может служить зеркальный цилиндр.
Таким образом, фотонная карта для caustic, являясь по сути все той же фотонной картой, имеет гораздо более высокое разрешение и хранится отдельно. По сложившейся терминологии, диффузные фотонные карты принято называть фотонными картами глобальной освещенности, в отличии от caustic фотонных карт.
Сaustic от внутренних отражающих стенок цилиндра при разном положении источников света.

Сaustic в результате преломления света прозрачным объектом. Фотонные карты позволяют сохранять данные о фотонах не только для полигональных поверхностей, но и для параметрических. В данном случае диффузная поверхность – песок, являющийся фрактальным параметрическим объектом.

Johan Thorngren. Сaustic в результате преломления света прозрачным объектом.
Второй проход. Модифицированный стохастический рейтресинг
На втором проходе вычисляется цвет пикселов, формирующих на экране конечное изображение. Для этого используется модифицированный метод стохастического (distribution) рейтресинга, описанный в первой части. Все происходит обычным способом вплоть до момента нахождения точки пересечения лучей от наблюдателя с поверхностью. Освещенность и цвет точки поверхности вычисляется теперь следующим образом. Во-первых, рассчитывается освещенность от прямых источников света обычным для рейтресинга способом. Если используются теневые фотоны, количество сэмплирующих источников света лучей может быть значительно уменьшено – более чем на 90 %. Вычисленная прямая освещенность составляет первую часть общей освещенности точки поверхности. Во-вторых, опять-таки традиционным для стохастического рейтресинга способом, рассчитываются вклады освещенности вдоль идеальных (и близких к идеальным) углов отражения и преломления – specular и glossy отражения и преломления. Напомню, что для этого используется specular-часть BRDF (BTDF) поверхности, которая сэмплируется дополнительными лучами. В конце траектории луча отражения/преломления находится диффузная поверхность. Освещенность в этой точке включает расчет прямого освещения, caustic (если есть) и вторичного отраженного освещения. Таким образом фотонные карты позволяют рассчитывать более точно отражения и преломления и в частности, видеть отражения/преломления caustic и радиосити. Это вторая составляющая освещенности точки. Фотонные карты могут быть использованы на этом этапе еще и следующим образом: поскольку фотонная карта поверхности хранит направления фотонов, анализ таких направлений в некоторой окрестности точки может быть использован для выбора оптимальных направлений importance-сэмплирующих лучей и ограничения шагов рекурсии стохастического рейтресинга, что значительно увеличивает как точность, так и скорость расчетов. По некоторым оценкам, величина шума в этом случае может быть уменьшена на 70 %.
Учет направлений фотонов, сохраненных в фотонной карте, позволяет эффективно выбирать направления сэмплирования, что уменьшает шум. Верхнее изображение – прямая визуализация фотонных карт, среднее изображение – использование обычного importance sampling, нижнее изображение – сэмплирование с учетом направлений, взятых из фотонных карт.
Третья составляющая – caustic-отражение, если оно имеет место для данной поверхности. Для визуализации освещенности используется caustic фотонная карта, подготовленная на первом проходе. Данные caustic фотонной карты отображаются без дополнительной обработки, напрямую. Это основная причина, по которой количество используемых для создания caustic фотонной карты лучей в десятки раз должно превосходить количество лучей для фотонных карт глобальной освещенности. Наконец, четвертая, и последняя, составляющая освещенности точки поверхности – вторичное освещение точки светом, многократно отраженным окружающими поверхностями. Да, это радиосити, но не только. Традиционно радиосити – это вторично диффузно отраженный свет. В нашем же случае кроме диффузно отраженного света может быть учтен и многократно зеркально (или вблизи идеальных углов) отраженный/преломленный другими поверхностями свет. Например, фотон мог отразиться диффузно от первой поверхности, затем – зеркально от второй поверхности и после этого попасть в рассматриваемую точку и опять диффузно рассеяться. Записи обо всех таких фотонах и им подобных уже хранятся в фотонной карте глобального освещения поверхности, освещенность точки которой рассматривается. Главное требование для того, чтобы фотон попал в базу данных – он должен быть диффузно рассеян данной поверхностью, и неважно, каким образом – по какой траектории и в результате каких взаимодействий с другими поверхностями, он сюда попал. Таким образом, фотонная карта глобальной освещенности простым и совершенно естественным образом позволяет учитывать любое вторичное отражение, диффузно рассеянное данной поверхностью! Для расчета диффузной освещенности точки (четвертой компоненты) необходимо выполнять интегрирование по окружающей точку полусфере всех входящих лучей вторичного освещения. Вместо этого используется фотонная карта данной поверхности. Вычисления выполняются так. В точке поверхности строится диск радиусом r таким, чтобы в пределах диска оказалось N (число N является задаваемым параметром точности вычислений) фотонов. Ближайшие к точке N фотонов находятся из фотонной карты глобальной освещенности данной поверхности. Тогда диффузная освещенность точки x вычисляется по формуле:
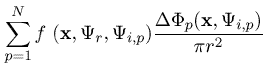
где:
N - заданное количество фотонов;
r - радиус диска поверхности, содержащего N фотонов.
Таким образом, мы опять имеем дело с методом Монте-Карло, заменяющим интеграл по сфере на сумму N значений подынтегральной функции, а фотонная карта глобальной освещенности помогает сделать оценку величины освещенности от вторичного отражения. Как обычно, чем больше число N (чем больше количество лучей от источника света, трассируемых на первом проходе), тем точнее оценка.
Сложив все четыре части мы получим окончательное значение освещенности точки поверхности для одного первичного луча. Приведенная схема вычисления освещенности является корректной с точки зрения математики, и точность расчетов будет зависеть только от количества лучей, сэмплирующих соответствующие интегралы уравнений освещенности. Именно такой способ расчетов, основанный на увеличении количества лучей, должен использоваться для получения точных значений освещенности, например в архитектурных визуализациях реальных проектов. В этом случае может потребоваться от нескольких сотен до нескольких тысяч лучей на пиксел, испускаемых от источников света на первом проходе (при прямом рейтресинге).
Если точность расчетов не важна, а значение имеет лишь правдоподобие изображения и время расчетов, может быть использована упрощенная схема, не требующая такого большого количества лучей. Этот метод расчетов получил название final gathering (окончательный сбор). Final gathering (FG) используется для вычисления четвертой компоненты освещенности – от вторичных отражений окружения точки. FG не использует для этого фотонную карту глобальной освещенности поверхности, которой принадлежит рассматриваемая точка, как в предыдущем случае. Вместо этого в точке строится сфера единичного радиуса, которая сэмплируется лучами в направлении окружения под случайными углами (направления сэмплирования могут быть выбраны с учетом направлений фотонной карты). Для каждого луча находится пересечение с поверхностью, и в каждой точке пересечения вычисляется диффузная освещенность при помощи фотонной карты глобального освещения этой поверхности (аналогично тому, как это было описано выше). Найденные значения складываются с некоторыми весовыми коэффициентами, и такая сумма и будет представлять оценку освещенности исходной точки.
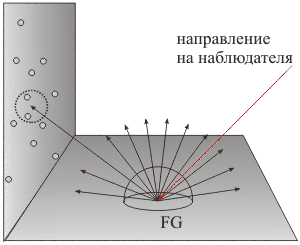
Схема сэмплирования final gathering
Метод FG позволяет почти в 10 раз уменьшить количество лучей прямого рейтресинга (используемых на первом проходе для построения фотонных карт глобальной освещенности) без появления заметного шума. Кроме того, FG вовсе не обязательно рассчитывать для каждой точки поверхности, достаточно вычислить в нескольких и затем интерполировать и экстраполировать методом градиентов диффузную освещенность между такими точками (этот прием предложен Greg Ward, автором известной программы рендеринга RADIANCE). В результате получается приличная экономия времени расчетов, а градиенты обеспечивают "красивый" сглаженный вид рендера.
Слева – прямая визуализация фотонных карт с 1 миллионом первичных фотонов (N=800), справа – использование FG, число лучей сэмплирования=800.
Однако, FG не является корректным способом расчета, а лишь его подделкой – "fake", поскольку учитывает далеко не всю освещенность, в отличие от фотонных карт и прямого рейтресинга. Из способа расчетов FG следует, что совсем не учитываются фотоны, отраженные зеркальными объектами (поскольку в этом случае соответствующие фотонные карты не сохраняют записей о них) и диффузно рассеянные рассматриваемой поверхностью. Кроме того, Final Gathering дает неплохие результаты в сценах с плавно изменяющейся вторичной рассеянной освещенностью и плохо справляется с ситуациями, когда имеются резкие перепады освещенности. Тем не менее, очевидно, что без FG в большинстве случаев просто не обойтись, может быть только когда производительность компьютеров увеличится еще на несколько порядков…
Вычисление вторичной освещенности методом фотонных карт, в отличие от расчета радиосити методом ограниченных поверхностей (разбиением на патчи), может быть выполнено для любой сколь угодно сложной геометрии. Традиционное вычисление радиосити очень сильно зависело от геометрии сцены и для сложных сцен была попросту невозможна. Фотонные карты не только полностью избавлены от этого недостатка, но и скорость расчетов методом фотонных карт почти не зависит от геометрии сцены, а только от количества лучей рейтресинга.
Учет взаимодействия света со средой
До сих пор предполагалось, что свет распространяется в вакууме, то есть не взаимодействует со средой, окружающей объекты. Для учета такого взаимодействия необходимо несколько модифицировать алгоритм расчета освещенности методом фотонных карт.
Представим себе ситуацию, когда луч света распространяется из точки 1 в точку 2 в вакууме. Пренебрегая ослаблением луча с расстоянием, можно сказать, что интенсивность света в точке 1 равна интенсивности света в точке 2. То есть, цвет и интенсивность луча неизменны вдоль всей его длины от точки 1 до точки 2. Если луч распространяется в некоторой среде, например – в наполненном пылью воздухе, он будет взаимодействовать со средой в каждой точке своей траектории. Такое взаимодействие будет приводить к изменению интенсивности и цвета по всей длине луча. Таким образом, можно сказать, что учет взаимодействия со средой приводит к необходимости расчета изменений интенсивности и цвета луча вдоль каждой точки траектории его распространения. Такое вычисление может быть проделано при помощи механизма, получившего название ray marching: траектория луча разбивается промежуточными точками на фиксированные по длине интервалы, и в каждой точке вычисляется изменение интенсивности луча.
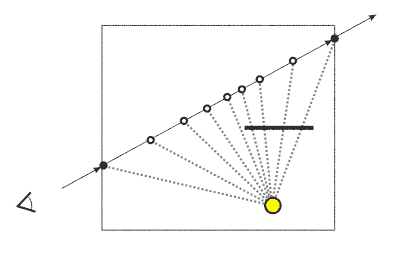
Ray marching
При этом считается, что изменения интенсивности луча вызваны:
а) ослаблением луча в результате его взаимодействия со средой (рассеяния и поглощения на частицах среды);
б) добавкой в результате освещения прямым источником света частиц среды на траектории луча;
в) добавкой в результате рассеяния света на окружающих траекторию луча частицах.
Для характеристики свойств среды вводятся новые величины:
s(x) – функция, определяющая вероятность рассеяния света (фотонов) на частицах среды в точке x;
p(x) – функция, определяющая вероятность поглощения фотона средой в точке x;
k(x) = s(x) + p(x);
NPF(x, n1, n2) – нормализованная фазовая функция, определяющая вероятность отражения средой фотона, приходящего в точку x под углом n1, на угол n2.
Для расчетов объемных световых эффектов также вводится объемная фотонная карта. Таким образом, в вычислениях будут задействованы теперь уже три типа фотонных карт: глобальные фотонные карты освещенности для поверхностей объектов, caustic фотонные карты для поверхностей и объемная фотонная карта для среды.
Объемная фотонная карта среды рассчитывается прямым рейтресингом от источников освещения на первом проходе, так же как и остальные типы фотонных карт. При этом, конечно же, взаимодействие лучей со средой сказывается и на остальных типах фотонных карт, поскольку лучи меняют свое направление и поглощаются средой. Каждый луч, распространяющийся от источника света в среде, может провзаимодействовать со средой в некоторой точке x – поглотиться в этой точке или рассеяться на некоторый угол. Вероятность взаимодействия луча (точнее – фотона, распространяющегося вдоль данной траектории) со средой в произвольной точке x определяется следующей формулой, получившей название оператора переноса:
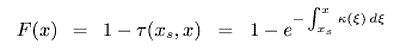
Если фотон взаимодействует со средой, и он идет не от источника света (то есть уже испытал хотя бы одно отражение), он сохраняется в объемной фотонной карте. Вид взаимодействия со средой – поглощение или рассеяние, определяется при помощи Русской рулетки. Вероятность того, что фотон будет рассеян, определяется соотношением s(x)/k(x), а направление распространения рассеянного фотона определяется фазовой функцией среды NPF (x, n1, n2). Построенная объемная фотонная карта используется на втором проходе для оценки вклада освещенности, отраженной на окружающих луч частицах среды. Для этого точка луча окружается сферой с таким радиусом, чтобы она содержала N фотонов, тогда вклад рассеянного освещения в эту точку рассчитывается по формуле:
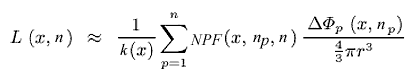
здесь L – добавка от рассеянного средой освещения,
энергия фотона из объемной фотонной карты в пределах сферы, окружающей точку пространства x;
r – радиус сферы, содержащей N фотонов вблизи x;
np и n – направления падения фотона с индексом p и направление луча соответственно.
Эта формула очень похожа по виду на ту, которая используется для расчета вторичного освещения точки поверхности.
На втором проходе, при расчете методом обратного рейтресинга, рассчитываются изменения интенсивности каждого луча, проходящего через среду методом ray marching. Луч разбивается на m интервалов, тогда изменение освещенности в промежуточных точках будет вычисляться итеративно:
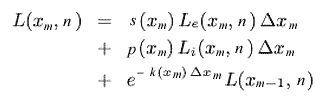
здесь первое слагаемое – вклад от освещенности частиц среды прямым источником света;
второе слагаемое – вклад рассеянного частицами среды освещения;
третье слагаемое – исходная интенсивность (интенсивность, вычисленная на предыдущей точке траектории).
Размер интервала автоматически делится пополам, если интенсивности луча в соседних точках сильно отличаются. Кроме того, длины интервалов немного отличаются случайным образом друг от друга (jittering), чтобы избежать алиасинга.
Таким образом, при расчете освещенности трехмерных сцен с учетом объемных эффектов взаимодействия света со средой строится три фотонных карты. Освещенность на поверхности объектов вычисляется методом фотонных карт и изменяется при переносе вдоль лучей в среде методом объемных фотонных карт. Используя вышеописанный алгоритм расчетов, совершенно естественным образом просчитываются самые разные объемные эффекты – светящийся ореол вокруг источников света, дым, облака, объемные caustic и другое.

Henrik Wann Jensen. Объемный caustic и светящийся ореол вокруг точечного источника света в среде, заполненной пылью. Расчет изображения выполнен в mental ray.

Henrik Wann Jensen. Cornell box с отражающей и прозрачной преломляющей сферами. Пространство заполнено пылевой средой и дымом. Расчет изображения выполнен в mental ray.

Henrik Wann Jensen. Облако, как пример расчета освещенности в неоднородной среде. Расчет изображения выполнен в mental ray.

Henrik Wann Jensen. Солнечные лучи, проникающие в комнату через цветной стеклянный витраж. Расчет изображения выполнен в mental ray.
Распространение света в материалах (subsurface scattering, translucent)
Воздух, заполненный пылью или дымом, представляет собой один полюс объемных сред, в которых свет взаимодействует с окружением. На другом полюсе находятся твердые органические и неорганические материалы. В компьютерной графике априори используется подход, согласно которому свойства взаимодействия света с твердыми непрозрачными объектами определяются исключительно свойствами поверхности таких материалов, или математически – BRDF. На самом деле, в реальности свет всегда проникает на некоторую глубину объема объекта в некоторой точке поверхности, взаимодействует с материалом (рассеивается или поглощается) внутри объема и выходит через поверхность наружу в другой точке поверхности, отличной от точки вхождения. При этом меняется как интенсивность, так и цвет отраженного света. Это физическое явление получило название подповерхностного переноса света – subsurface scattering, еще его называют translucency.
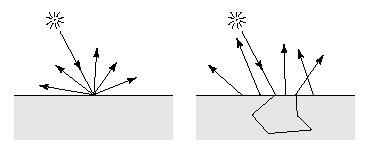
Слева - взаимодействие света с объектом, предполагаемое при использовании модели BRDF, справа - subsurface scattering (BSSDRF).
Взаимодействие света с объемом объекта неважно для неорганических материалов, таких как металл, и в этом случае достаточно обычной BRDF. Однако, эффекты subsurface scattering исключительно важны для всех органических материалов. Неучет этого эффекта особенно губителен для реалистичного восприятия смоделированных на компьютере изображений кожи, фруктов, молока и т.д. и т.п. В доказательство хочу привести два изображения кожи, рассчитанных с использованием обычного подхода (только поверхностная функция BRDF) и с учетом subsurface scattering:

Henrik Wann Jensen. Кожа лица рассчитанная при помощи BRDF. Даже с использованием глобальной освещенности кожа имеет явно выраженный синтетический вид и больше напоминает резину.

Henrik Wann Jensen. Кожа лица рассчитана с учетом подповерхностного рассеяния (subsurface scattering) и даже без глобального освещения гораздо больше похожа на то, что мы наблюдаем в жизни. Обратите внимание на очень натуралистичные цветовые переходы на границе тени под носом, здесь кожа почти светится!
Для фотореалистичного моделирования органических объектов subsurface scattering просто необходим, без него не обойтись.
Для учета subsurface scattering необходимо обобщить BRDF таким образом, чтобы новая фикция описывала взаимосвязь угла падения света на поверхность объекта в данной точке с углом и точкой выхода на поверхность света из глубины объекта после взаимодействия. Такая функция получила название BSSDRF (bidirectional surface scattering reflectance distribution function). В настоящее время наиболее совершенной BSSDRF в компьютерной графике считается модель, разработанная Henrik Wann Jensen. Эта модель предполагает следующее поведение света: луч падает на поверхность объекта и испытывает отражение Фреснеля, обусловленное переходом света в другую среду, описывается относительным коэффициентом преломления на границе двух сред. Далее свет проникает в объем на некоторую глубину, которая определяется коэффициентом поглощения и рассеяния материала объекта. Свет может быть поглощен или рассеян. Рассеяние света может быть однократным, в этом случае свет выходит на поверхность и покидает ее под некоторым определенным углом (так называемое однократное направленное рассеяние). Свет может также многократно рассеиваться в объеме материала. В этом случае лучи с равной вероятностью могут выйти на поверхность под любым углом – это диффузное рассеяние света в объеме материала. Поэтому, BSSDRF состоит из двух частей – первая часть функции описывает диффузное рассеяние, вторая часть описывает однократное направленное рассеяние. Jensen вывел математическую формулу, с помощью которой можно построить BSSDRF произвольного материала для объектов любой геометрии, достаточно точно согласующуюся с экспериментальными данными. Явный вид этой формулы я приводить здесь не буду, по той причине, что он сложен и не отличается интуитивностью. Гораздо важнее то, что современные рендеры используют эту модель и позволяют создать объемный шейдер, если известны такие характеристики материала как:
коэффициент поглощения;
коэффициент рассеяния;
величина изотропности рассеяния g; g=0 для изотропного рассеяния (равномерного по всем направлениям), для других значений g рассеяние будет преимущественно вперед или назад относительно направления распространения луча в объеме.
Обобщение BRDF до BSSDRF требует модификации алгоритма расчетов. К счастью, такая модификация может быть сделана естественным образом в рамках классического distribution raytracing. А именно, при пересечении первичного луча от наблюдателя с поверхностью в случае BRDF источник света сэмплируется лучами из одной точки поверхности. Для вычисления BSSDRF требуется испускать такие лучи из разных точек в малой окрестности точки пересечения первичного луча с поверхностью для вычисления диффузной части и сэмплировать свет из разных точек на линии преломленного выходящего луча для расчета однократно рассеянного излучения. Все точки выбираются при помощи коэффициентов поглощения и рассеяния среды. Расчет освещенности предполагает вычисление только прямого освещения, глобальное освещение не рассчитывается.
Mental ray обладает объемным шейдером типа parti_volume, основанном на модели BSSDRF Йенсена. Шейдер parti_volume интересен еще и тем, что обладает тремя параметрами, сочетание которых позволяет задавать размер частиц среды и тем самым определить тип объемного рассеяния. Если размеры частицы много меньше длины волны света, среда будет почти идеально поглощающей. Если размер частиц немного меньше длины волны света – среда представляет собой сигаретный дым или пыль (тип рассеяния – Rayleigh). Если частицы по размеру приблизительно одинаковы с длиной волны, среда – водяная пыль или туман с типом рассеяния Mie. Наконец, если размеры частиц намного превосходят длину волны, мы имеем дело с твердыми органическими и неорганическими материалами.
Final render также имеет некоторые настройки translucent-материалов, хотя в последнем случае насчет используемой модели BSSDRF я не уверен (и уж точно эту модель не использует стандартный translucent-материал 3ds max).
Позволю себе привести еще несколько примеров рендеров на основе модели BSSDRF Хенрика ван Йенсена:

Стакан молока. Изображение получено при помощи BRDF и глобальной модели освещенности. Напоминает скорее стакан с белой краской.

Тот же стакан молока, на сей раз используется BSSRDF. Интересно, что в данном случае воспроизведены не только изменения прозрачности молока вблизи поверхности, но даже такие тонкости, как изменение цвета с глубиной. Ближе к фронту молоко имеет красноватый оттенок, а дальше к заднему плану приобретает голубоватый цвет.

Стакан молока, используется BSSRDF с другими свойствами поглощения и рассеяния материала (цельное молоко). Можно считать это доказательством того, что модель BSSRDF вполне в состоянии реалистично воспроизводить не только разные материалы, но и разные сорта одного материала.
Дальнейшее развитие модели BSSDRF предполагает учет глобального, а не только прямого, освещения и введение в модель нескольких слоев материала.
Заключение
Развитие алгоритмов рендеринга прошло довольно большой путь: локальная модель освещения, райтресинг, радиосити, метод фотонных карт – вот основные вехи этой эволюции. Метод обратного рейтресинга появился как результат отказа от прямого прослеживания траекторий света от источника до наблюдателя. Забавно то, что по мере совершенствования приемов рендеринга, придя к фотонным картам, мы вернулись и к необходимости использования прямого рейтресинга. Развитие происходит по спирали, что еще раз и подтвердила практика. Расчет освещенности методом фотонных карт является на сегодняшний день "state of the art", сочетающим все основные преимущества предшественников – обратный рейтресинг и антиалиасинг, вторичное освещение (радиосити) и прямую трассировку лучей. Метод фотонных карт позволяет, в принципе, воспроизвести на компьютере почти все явления геометрической оптики. По-видимому, по крайней мере в ближайшее время, эволюция рендеринга будет связана с дальнейшим совершенствованием алгоритмов фотонных карт, потенциал неиспользованных возможностей здесь еще довольно велик. Так, в качестве одного из примеров такого развития можно упомянуть Metropolis Light Transport, оптимизирующий способ прямой трассировки лучей выбором значимых по вкладу лучевых траекторий. Это позволяет рассчитывать освещенность с тем же качеством, что и стандартный (теперь уже) метод фотонных карт, но за меньшее время. Другим новым перспективным направлением является Image Based Rendering, использующий в качестве источника освещения HDR-изображения. Эта техника уже довольно широко применяется в кино.
Однако, существует целый класс проблем, который в рамках существующей модели переноса света неразрешим в принципе. Это проблемы, обусловленные волновой природой света. Такие, например, как дифракция и интерференция света. Без расширения модели их не решить.
Таким образом, скорее всего, дальнейшее развитие рендеринга будет проходить в направлении совершенствования существующих алгоритмов, и прежде всего – ускорения расчетов в том числе для целей интерактивной графики; а также, в направлении расширения существующей модели переноса света. Исследования в этой области ведутся довольно интенсивно, так что я думаю, новые темы для обсуждения не должны заставить себя долго ждать.













